A transition function \(G(r,\theta,\phi)\) with \(f(r,\theta,\phi)\) that falls off linearly from an inner surface of a wedge to an outer surface of a wedge. Meant to be used in domain::CoordinateMaps::Wedge blocks.
More...
#include <Wedge.hpp>
Public Types | |
| enum class | Axis : int { Interior = 4 , PlusZ = 3 , MinusZ = -3 , PlusY = 2 , MinusY = -2 , PlusX = 1 , MinusX = -1 , None = 0 } |
| Class to represent the direction of the wedge relative to the outer center. More... | |
Public Member Functions | |
| Wedge (const std::array< double, 3 > &inner_center, double inner_radius, double inner_sphericity, const std::array< double, 3 > &outer_center, double outer_radius, double outer_sphericity, Axis axis, bool reverse=false) | |
| Construct a Wedge transition for a wedge block in a given direction. More... | |
| double | operator() (const std::array< double, 3 > &source_coords, const std::optional< size_t > &one_over_radius_power) const override |
| DataVector | operator() (const std::array< DataVector, 3 > &source_coords, const std::optional< size_t > &one_over_radius_power) const override |
| std::optional< double > | original_radius_over_radius (const std::array< double, 3 > &target_coords, double radial_distortion) const override |
| The inverse of the transition function. More... | |
| std::array< double, 3 > | gradient (const std::array< double, 3 > &source_coords) const override |
| std::array< DataVector, 3 > | gradient (const std::array< DataVector, 3 > &source_coords) const override |
| WRAPPED_PUPable_decl_template (Wedge) | |
| Wedge (CkMigrateMessage *msg) | |
| void | pup (PUP::er &p) override |
| std::unique_ptr< ShapeMapTransitionFunction > | get_clone () const override |
| bool | operator== (const ShapeMapTransitionFunction &other) const override |
| bool | operator!= (const ShapeMapTransitionFunction &other) const override |
 Public Member Functions inherited from domain::CoordinateMaps::ShapeMapTransitionFunctions::ShapeMapTransitionFunction Public Member Functions inherited from domain::CoordinateMaps::ShapeMapTransitionFunctions::ShapeMapTransitionFunction | |
| virtual std::optional< double > | original_radius_over_radius (const std::array< double, 3 > &target_coords, double radial_distortion) const =0 |
| The inverse of the transition function. More... | |
| virtual std::unique_ptr< ShapeMapTransitionFunction > | get_clone () const =0 |
| virtual bool | operator== (const ShapeMapTransitionFunction &other) const =0 |
| virtual bool | operator!= (const ShapeMapTransitionFunction &other) const =0 |
| WRAPPED_PUPable_abstract (ShapeMapTransitionFunction) | |
| ShapeMapTransitionFunction (CkMigrateMessage *m) | |
Friends | |
| std::ostream & | operator<< (std::ostream &os, Axis axis) |
Detailed Description
A transition function \(G(r,\theta,\phi)\) with \(f(r,\theta,\phi)\) that falls off linearly from an inner surface of a wedge to an outer surface of a wedge. Meant to be used in domain::CoordinateMaps::Wedge blocks.
Details
The functional form of this transition is
\begin{equation} G(r,\theta,\phi) = \frac{f(r,\theta,\phi)}{r} \label{eq:transition_func} \end{equation}
where
\begin{equation} f(r, \theta, \phi) = \frac{D_{\text{out}}(r, \theta, \phi) - r}{D_{\text{out}}(r, \theta, \phi) - D_{\text{in}}(r, \theta, \phi)}, \label{eq:linear_transition_func} \end{equation}
where, in general,
\begin{equation} D(r, \theta, \phi) = R\left(\frac{1 - s}{\sqrt{3}\max(|\sin{\theta}\cos{\phi}|,|\sin{\theta}\sin{\phi}|, |\cos{\theta}|)} + s\right). \label{eq:distance} \end{equation}
Here, \(s\) is the sphericity of the surface which goes from 0 (flat) to 1 (spherical), \(R\) is the radius of the spherical surface, \(\text{out}\) is the outer surface, and \(\text{in}\) is the inner surface. If the sphericity is 1, then the surface is a sphere so \(D = R\). If the sphericity is 0, then the surface is a cube. This cube is circumscribed by a sphere of radius \(R\). See domain::CoordinateMaps::Wedge for more of an explanation of these boundary surfaces and their sphericities.
- Note
- If
reverseis true, then the functional form of the transition is actually\begin{equation} f(r, \theta, \phi) = 1 - \frac{D_{\text{out}}(r, \theta, \phi) - r}{D_{\text{out}}(r, \theta, \phi) - D_{\text{in}}(r, \theta, \phi)} = \frac{r - D_{\text{in}}(r, \theta, \phi)} {D_{\text{out}}(r, \theta, \phi) - D_{\text{in}}(r, \theta, \phi)}. \label{eq:linear_transition_func_reverse} \end{equation}
- Note
- Because the shape map distorts only radii and does not affect angles, \(D\) is not a function of \(r\) so we have that \(D(r,\theta,\phi) = D(\theta, \phi)\).
The transition function is also defined within \(D_{\text{in}}(r, \theta, \phi)\) if the axis is Axis::Interior. Within \(D_{\text{in}}(r, \theta, \phi)\), the transition function is
\begin{equation} \label{eq:interior_transition_func} G(r,\theta,\phi) = \frac{r^2}{D_{\text{in}}(r, \theta, \phi)^3} = \frac{r^3}{R_0^3} \end{equation}
and none of the vector formulation is necessary. This is chosen to match Eq. \(\ref{eq:transition_func}\) at \(D_{\text{in}}(r, \theta, \phi)\) and go to 0 at \(r=0\). The second equality is explained by one of the following bullets.
There are several assumptions made for this mapping:
- The coordinates \(r, \theta, \phi\) are assumed to be from the center of the inner surface, not the center of the computational domain.
- The wedges are concentric. (see the constructor) This is also enforced by the center of the inner surface being within the outer surface.
- If the centers of the inner and outer surface are different, then the inner sphericity must be 1 (i.e. \(D_{\text{in}} = R\)).
- If the axis is
Axis::Interior, then the inner sphericity must be 1 andreversemust be false. - The \(\max\) in the denominator of \(\ref{eq:distance}\) can be simplified a bit to \(\max(|x|, |y|, |z|)/r\). It was written the other way in \(\ref{eq:distance}\) to emphasize that \(D\) has no radial dependence.
Vector formulation
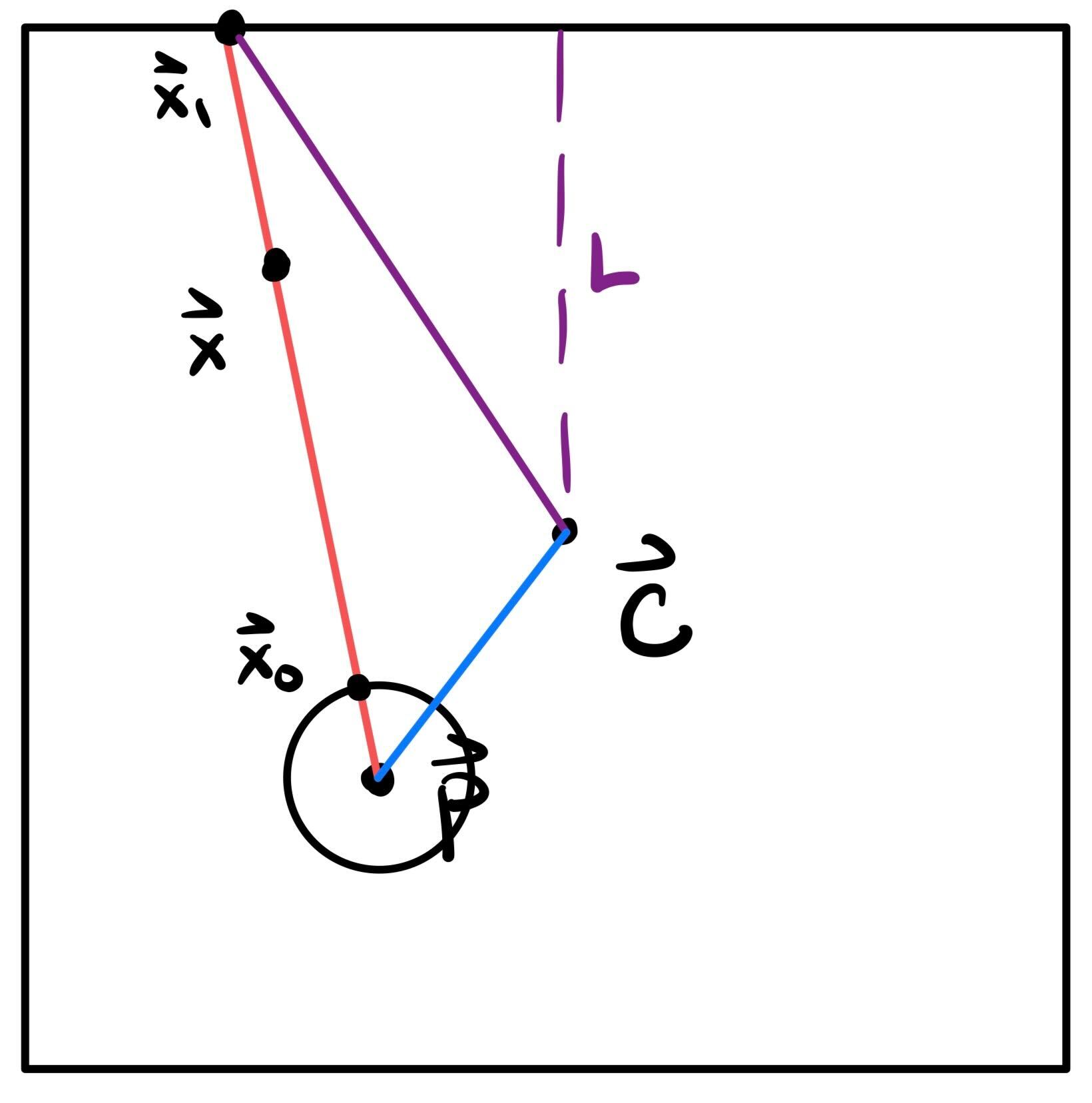
It can be more convenient to work with vectors rather than just distances for the following equations. Therefore, we define the projection center \(\vec P\) which points from the center of the outer surface to the center of the inner surface. If the centers of the inner and outer surface are the same, then \(\vec P = 0\). Then, we define \(\vec x\) as the vector from the center of the outer surface to the coordinate we are interested in. We define \(\vec x_0\) as the vector from the center of the outer surface to the point along ray \(\vec x - \vec P\) which intersects the inner surface. Similarly, \(\vec x_1\) intersects the outer surface along the same ray as \(\vec x - \vec P\). Any cube has a side length of \(2L\).
In this way, we can reformulate Eq. \(\ref{eq:linear_transition_func}\) as
\begin{equation}\label{eq:linear_transition_func_vec} f(\vec x) = \frac{|\vec x_1 - \vec P| - r}{|\vec x_1 - \vec P| - |\vec x_0 - \vec P|} \end{equation}
where
\begin{equation} r = |\vec x - P| \end{equation}
Computing vector to inner surface
Similar to Eq. \(\ref{eq:distance}\) we can define \(\vec x_0\) as
\begin{equation}\label{eq:x_0_vector} \vec x_0 = R_0\left( \frac{r(1-s_0)}{\sqrt{3}\max{(x_i - P_i)}} + s\right) \hat r + \vec P \end{equation}
with
\begin{equation} \hat r = \frac{\vec x - \vec P}{|\vec x - \vec P|}. \end{equation}
and also
\begin{equation}\label{eq:x_0_norm} |\vec x_0 - \vec P| = R_0\left( \frac{r(1-s_0)}{\sqrt{3}\max{(x_i - P_i)}} + s_0\right) \end{equation}
Computing vector to outer surface
Then, we define
\begin{equation}\label{eq:x_1} \vec x_1 = \lambda (\vec x - \vec P) + \vec P \end{equation}
where \(\lambda\) is a scalar to be determined. We can see that this is valid because \(\vec x - \vec P\) is centered on \(\vec P\) and lies along the ray so \(\lambda\) will scale this vector to be the correct length.
Computing \(\lambda\) is a bit complicated because the outer surface can either be a cube, a sphere, or something in between and the way to solve for \(\lambda\) in the cube case is different than in the sphere case. Therefore we define \(\lambda_c\) and \(\lambda_s\) as the scalar factors for the cube and sphere case, respectively. This allows us to define \(\lambda\) as
\begin{equation}\label{eq:lambda} \lambda = (1 - s_1) \lambda_c + s_1 \lambda_s \end{equation}
Computing cube lambda
To compute \(\lambda_c\) for the cube case, we notice that (in the image)
\begin{align} L &= \vec x_1 \cdot \hat z \\ &= \left(\lambda_c^{+z}(\vec x - \vec P) + \vec P\right) \cdot \hat z\\ &= \lambda_c^{+z}(x_z - P_z) + P_z \end{align}
If we generalize this to all six unit vectors and solve for \(\lambda_c^{\pm k}\) we get
\begin{equation}\label{eq:lambda_c_pm} \lambda_c^{\pm k} = \frac{\pm L - \vec P \cdot \hat x_k}{(\vec x - \vec P) \cdot \hat x_k} \end{equation}
for \(k \in \{x, y, z\}\). This quantity \(\lambda_c^{\pm k}\) represents the factor needed to scale the vector \(\vec x - \vec P\) to intersect with the infinite planes that contain the six faces of the cube.
Some \(\lambda_c^{\pm k}\) will be negative as they point to the opposite planes. We can discard those. Then for the \(\lambda_c^{\pm k}\) that are positive, we want the one that is smallest in magnitude. This can be written as
\begin{equation}\label{eq:lambda_c} \lambda_c = \min_{\substack{\lambda_c^{\pm k} > 0}} (\lambda_c^{\pm k}) \end{equation}
Computing sphere lambda
To compute \(\lambda_s\) for the sphere case, again we notice that (in the image)
\begin{align} R_1^2 &= |\vec x_1|^2 \\ &= |\lambda_s (\vec x - \vec P) + \vec P|^2 \\ &= \lambda_s^2 |\vec x - \vec P|^2 + 2 \lambda_s (\vec x - \vec P) \cdot \vec P + |\vec P|^2 \end{align}
This is simply a quadratic equation for \(\lambda_s\):
\begin{equation}\label{eq:lambda_s} 0 = \lambda_s^2 |\vec x - \vec P|^2 + 2 \lambda_s (\vec x - \vec P) \cdot \vec P + |\vec P|^2 - R_1^2 \end{equation}
We explicitly don't write the typical form of the solution of a quadratic equation because that form behaviors poorly numerically if the two terms in the numerator are close to each other (bad numerical roundoff). Therefore, we just resolve to compute the solution numerically, and say that we have \(\lambda_s\).
We have now solved for \(\vec x_1\).
\begin{equation} \vec x_1 = \left((1 - s_1) \lambda_c + s_1 \lambda_s \right) (\vec x - \vec P) + \vec P \end{equation}
given the solutions for \(\lambda_c\) in Eqn. \(\ref{eq:lambda_c}\) and \(\lambda_s\) in Eqn. \(\ref{eq:lambda_s}\).
Original radius divided by mapped radius
Given an already mapped point \(\tilde{\vec x}\) and the radial distortion \(\Sigma(\theta, \phi) = \sum_{\ell,m}\lambda_{\ell m}Y_{\ell m}(\theta, \phi)\), we can figure out the ratio of the original radius \(r\) to the mapped \(\tilde{r} = |\tilde{\vec x}|\) by solving
\begin{equation} \frac{r}{\tilde{r}} = \frac{1}{1-G(r)\Sigma(\theta,\phi)} \end{equation}
If the axis is Axis::Interior, this formula becomes (after simplification and because the inner surface must be spherical)
\begin{equation} 0 = \left(\frac{r}{\tilde{r}}\right)^3 - \left(\frac{r}{\tilde{r}}\right) \frac{R_0^3}{\tilde{r}^2\Sigma(\theta,\phi)} + \frac{R_0^3}{\tilde{r}^2\Sigma(\theta,\phi)} \end{equation}
This is a special case of a cubic root, so we use the method outlined in [172] on pg 228.
For other axes, after plugging in \(f(r,\theta,\phi)/r\) and solving, we get
\begin{equation} \frac{r}{\tilde{r}} = \frac{1 + \frac{|\vec x_1 - \vec P|\Sigma(\theta, \phi)}{\tilde{r}(|\vec x_1 - \vec P| - |\vec x_0 - \vec P|)}}{1 + \frac{\Sigma(\theta, \phi)}{|\vec x_1 - \vec P| - |\vec x_0 - \vec P|}} \label{eq:r_over_rtil} \end{equation}
- Note
- Since \(\vec x_0 - \vec P\) and \(\vec x_1 - \vec P\) are not functions of the radius, we can use \(\tilde{\vec x}\) in Eq. \(\ref{eq:x_0_vector}\) instead of \(\vec x\).
- Note
- If
reverseis true, then the value multiplying \(\Sigma\) in the numerator is now \(-|\vec x_0 - \vec P|\) and in the denominator \(\Sigma\) picks up a minus sign factor.
Gradient
The cartesian gradient of the transition function is
\begin{equation} \frac{\partial G}{\partial x_i} = \frac{1}{r}\frac{\partial f}{\partial \xi^i} - \frac{f \xi_i}{r^3} \end{equation}
where
\begin{equation} \frac{\partial f}{\partial x_i} = \frac{\frac{\partial |\vec x_1 - \vec P|}{\partial x_i} - \frac{x_i - P_i}{r}}{|\vec x_1 - \vec P| - |\vec x_0 - \vec P|} - \frac{\left(|\vec x_1 - \vec P| - r\right)\left(\frac{\partial |\vec x_1 - \vec P|}{\partial x_i} - \frac{\partial |\vec x_0 - \vec P|}{\partial x_i} \right)}{\left(|\vec x_1 - \vec P| - |\vec x_0 - \vec P|\right)^2}. \end{equation}
- Note
- If
reverseis true, the gradient picks up an overall factor of -1.0.
If the axis is Axis::Interior, then the gradient is
\begin{equation} \frac{\partial G}{\partial x_i} = \frac{2(x_i-P_i)}{R_0^3} \end{equation}
For the other axes, we need to compute the gradients of \(\vec x_0\) and \(\vec x_1\).
Gradient of vector to inner surface
If \(\vec P \neq 0\), then we require the inner surface to be a sphere, which means the gradient is trivially zero. Therefore the following is only for when \(\vec P = 0\).
The gradient of \(|\vec x_0 - \vec P|\) depends on the result of the \(\max\) in the denominator of \(\ref{eq:x_0_norm}\). To simplify the expression, let \(i \in \{0,1,2\}\) correspond to the \(\max(x_i - P_i)\). Then we can write the gradient of as
\begin{align} \frac{\partial |\vec x_0 - \vec P|}{\partial x_i} &= -\text{sgn}(x_i - P_i)\frac{R(1-s)\left(r^2 - (x_i - P_i)^2\right)} {r (x_i - P_i)^2 \sqrt{3}} \\ \frac{\partial |\vec x_0 - \vec P|}{\partial x_{i+1}} &= \frac{R(1-s)(x_{i+1} - P_{i+1})}{r |x_i - P_i| \sqrt{3}} \\ \frac{\partial |\vec x_0 - \vec P|}{\partial x_{i+2}} &= \frac{R(1-s)(x_{i+2} - P_{i+2})}{r |x_i - P_i| \sqrt{3}} \end{align}
where \(i+1\) and \(i+2\) are understood to be \(\mod 3\). Also since we don't allow points at the center of the inner surfaces, we can be assured that for whichever \(i\) is max, that \(x_i - P_i\) won't be zero.
Gradient of vector to outer surface
This gradient is much more complicated because of how we have to define \(\lambda\). To start off with, we need to compute
\begin{align}\label{eq:x_1_grad} \frac{\partial}{\partial x_i}|\vec x_1 - \vec P| &= \frac{\partial}{\partial x_i} (\lambda |\vec x - \vec P|) \\ &= \frac{\lambda (x_i - P_i)}{|\vec x - \vec P|} + \frac{\partial \lambda}{\partial x_i}|\vec x - \vec P| \end{align}
Since we know \(\lambda\) and \(\vec x\), that just leaves
\begin{equation} \frac{\partial\lambda}{\partial x_i} = \frac{\partial\lambda_c}{\partial x_i}(1-s_1) + s_1\frac{\partial\lambda_s}{\partial x_i} \end{equation}
Gradient of cube lambda
Taking the gradient of Eqn. \(\ref{eq:lambda_c_pm}\) we notice that \(L\), \(\vec P\), and \(\hat x_k\) are constant, so we only have to worry about \(\vec x\)
\begin{equation}\label{eq:tmp_lambda_c_grad} \frac{\partial}{\partial x_i}\lambda_c^{\pm k} = -\frac{(\pm L - \vec P \cdot \hat x_k)(\partial/\partial x_i(\vec x - \vec P) \cdot \hat x_k)}{((\vec x - \vec P) \cdot \hat x_k)^2} \end{equation}
The gradient in the numerator is simple to take so we end up with
\begin{equation} \frac{\partial}{\partial x_i}\lambda_c^{\pm k} = -\frac{(\pm L - \vec P \cdot \hat x_k)}{( x_k - P_k)^2} \delta_{ik} \end{equation}
Gradient of sphere lambda
Taking the gradient of Eqn. \(\ref{eq:lambda_s}\) (and using the fact that \(\vec P\) and \(R\) are constant), we get
\begin{equation} 0 = \lambda_s \frac{\partial \lambda_s}{\partial x_i}|\vec x - \vec P|^2 + \lambda_s^2 (\vec x - \vec P) \cdot \frac{\partial}{\partial x_i}(\vec x - \vec P) + \frac{\partial\lambda_s}{\partial x_i}(\vec x - \vec P) \cdot \vec P + \lambda_s \vec P \cdot \frac{\partial}{\partial x_i}(\vec x - \vec P) \end{equation}
Taking the simple gradients and moving things around, we get
\begin{equation} \frac{\partial\lambda_s}{\partial x_i} = - \frac{\lambda_s^2 (x_i - P_i) + \lambda_s P_i}{\lambda_s |\vec x - \vec P|^2 + (\vec x - \vec P) \cdot \vec P} \end{equation}
where \(\lambda_s\) can be computed from Eqn. \(\ref{eq:lambda_s}\).
So now we can put it all together and we get
\begin{equation} \frac{\partial\lambda}{\partial x_i} = -\frac{(\pm L - \vec P \cdot \hat x_k)}{( x_k - P_k)^2} \delta_{ik}(1 - s_1) + s_1 \frac{\lambda_s^2 (x_i - P_i) + \lambda_s P_i}{\lambda_s |\vec x - \vec P|^2 + (\vec x - \vec P) \cdot \vec P} \end{equation}
which can then be substituted into Eqn. \(\ref{eq:x_1_grad}\) to get the gradient of \(|\vec x_1 - \vec P|\).
Member Enumeration Documentation
◆ Axis
|
strong |
Class to represent the direction of the wedge relative to the outer center.
Details
Interior means within inner surface.
Constructor & Destructor Documentation
◆ Wedge()
| domain::CoordinateMaps::ShapeMapTransitionFunctions::Wedge::Wedge | ( | const std::array< double, 3 > & | inner_center, |
| double | inner_radius, | ||
| double | inner_sphericity, | ||
| const std::array< double, 3 > & | outer_center, | ||
| double | outer_radius, | ||
| double | outer_sphericity, | ||
| Axis | axis, | ||
| bool | reverse = false |
||
| ) |
Construct a Wedge transition for a wedge block in a given direction.
Details
Many concentric wedges can be part of the same falloff from 1 at the inner boundary of the innermost wedge, to 0 at the outer boundary of the outermost wedge.
- Note
- If
inner_centerandouter_centerare different, theninner_sphericitymust be 1.0. if theaxisisAxis::Interior, theninner_sphericitymust be 1.0 andreversemust be false.
- Parameters
-
inner_center Center of the inner surface inner_radius Inner radius of innermost wedge inner_sphericity Sphericity of innermost surface of innermost wedge outer_center Center of the outer surface outer_radius Outermost radius of outermost wedge outer_sphericity Sphericity of outermost surface of outermost wedge axis The direction that this wedge is in. reverse If true, the function \(f\) will be 0 at the inner boundary and 1 at the outer boundary (useful for deforming star surfaces). Otherwise, it will be 1 at the inner boundary and 0 at the outer boundary (useful for deforming black hole excision surfaces).
Member Function Documentation
◆ get_clone()
|
inlineoverridevirtual |
◆ gradient() [1/2]
|
overridevirtual |
Evaluate the gradient of the transition function with respect to the Cartesian coordinates x, y and z at the Cartesian coordinates source_coords.
Implements domain::CoordinateMaps::ShapeMapTransitionFunctions::ShapeMapTransitionFunction.
◆ gradient() [2/2]
|
overridevirtual |
Evaluate the gradient of the transition function with respect to the Cartesian coordinates x, y and z at the Cartesian coordinates source_coords.
Implements domain::CoordinateMaps::ShapeMapTransitionFunctions::ShapeMapTransitionFunction.
◆ operator!=()
|
overridevirtual |
◆ operator()() [1/2]
|
overridevirtual |
Evaluate the transition function \(G(r,\theta,\phi)\) at the Cartesian coordinates source_coords and possibly divide by the radius \(r\).
Details
If one_over_radius_power has a value, then divide \(G\) by \(r\) to that power. This is done here because the transition function knows how to handle points in various regions of the map.
Implements domain::CoordinateMaps::ShapeMapTransitionFunctions::ShapeMapTransitionFunction.
◆ operator()() [2/2]
|
overridevirtual |
Evaluate the transition function \(G(r,\theta,\phi)\) at the Cartesian coordinates source_coords and possibly divide by the radius \(r\).
Details
If one_over_radius_power has a value, then divide \(G\) by \(r\) to that power. This is done here because the transition function knows how to handle points in various regions of the map.
Implements domain::CoordinateMaps::ShapeMapTransitionFunctions::ShapeMapTransitionFunction.
◆ operator==()
|
overridevirtual |
◆ original_radius_over_radius()
|
overridevirtual |
The inverse of the transition function.
This method returns \(r/\tilde{r}\) given the mapped coordinates \(\tilde{x}^i\) (target_coords) and the spherical harmonic expansion \(\Sigma(t, \theta, \phi) = \sum_{lm} \lambda_{lm}(t)Y_{lm}(\theta, \phi)\) (radial_distortion). See domain::CoordinateMaps::TimeDependent::Shape for details on how this quantity is used to compute the inverse of the Shape map.
To derive the expression for this inverse, solve Eq. ( \(\ref{eq:shape_map_radius}\)) for \(r\) after substituting \(G(r,\theta,\phi)\).
- Parameters
-
target_coords The mapped Cartesian coordinates \(\tilde{x}^i\). radial_distortion The spherical harmonic expansion \(\Sigma(t, \theta, \phi)\).
Returns: The quantity \(r/\tilde{r}\).
Implements domain::CoordinateMaps::ShapeMapTransitionFunctions::ShapeMapTransitionFunction.
The documentation for this class was generated from the following file:
- src/Domain/CoordinateMaps/TimeDependent/ShapeMapTransitionFunctions/Wedge.hpp