domain::CoordinateMaps::Wedge< Dim > Class Template Reference

Map from a square or cube to a wedge. More...

#include <Wedge.hpp>

Public Types
enum class	WedgeHalves { Both , UpperOnly , LowerOnly }

Public Member Functions
	Wedge (double radius_inner, double radius_outer, double sphericity_inner, double sphericity_outer, OrientationMap< Dim > orientation_of_wedge, bool with_equiangular_map, WedgeHalves halves_to_use=WedgeHalves::Both, Distribution radial_distribution=Distribution::Linear, const std::array< double, Dim - 1 > &opening_angles=make_array< Dim - 1 >(M_PI_2), bool with_adapted_equiangular_map=true)
	Constructs a centered wedge (one with no focal offset) More...
	Wedge (double radius_inner, std::optional< double > radius_outer, double cube_half_length, std::array< double, Dim > focal_offset, OrientationMap< Dim > orientation_of_wedge, bool with_equiangular_map, WedgeHalves halves_to_use=WedgeHalves::Both, Distribution radial_distribution=Distribution::Linear)
	Constructs a wedge with a focal offset. More...
	Wedge (Wedge &&)=default
	Wedge (const Wedge &)=default
Wedge &	operator= (const Wedge &)=default
Wedge &	operator= (Wedge &&)=default
template<typename T >
std::array< tt::remove_cvref_wrap_t< T >, Dim >	operator() (const std::array< T, Dim > &source_coords) const
std::optional< std::array< double, Dim > >	inverse (const std::array< double, Dim > &target_coords) const
	For a \(+z\)-oriented Wedge, returns invalid if \(z<=0\) or if \((x,y,z)\) is on or outside the cone defined by \((x^2/z^2 + y^2/z^2+1)^{1/2} = -S/F\), where \(S = \frac{1}{2}(s_1 r_1 - s_0 r_0)\) and \(F = \frac{1}{2\sqrt{3}}((1-s_1) r_1 - (1-s_0) r_0)\). Here \(s_0,s_1\) and \(r_0,r_1\) are the specified sphericities and radii of the inner and outer \(z\) surfaces. The map is singular on the cone and on the xy plane. The inverse function is only callable with doubles because the inverse might fail if called for a point out of range, and it is unclear what should happen if the inverse were to succeed for some points in a DataVector but fail for other points.
template<typename T >
tnsr::Ij< tt::remove_cvref_wrap_t< T >, Dim, Frame::NoFrame >	jacobian (const std::array< T, Dim > &source_coords) const
template<typename T >
tnsr::Ij< tt::remove_cvref_wrap_t< T >, Dim, Frame::NoFrame >	inv_jacobian (const std::array< T, Dim > &source_coords) const
void	pup (PUP::er &p)

Static Public Member Functions
static constexpr bool	is_identity ()

Static Public Attributes
static constexpr size_t	dim = Dim

Friends
template<size_t LocalDim>
bool	operator== (const Wedge< LocalDim > &lhs, const Wedge< LocalDim > &rhs)

Detailed Description

template<size_t Dim>
class domain::CoordinateMaps::Wedge< Dim >

Map from a square or cube to a wedge.

A shell can be constructed out of six wedges.

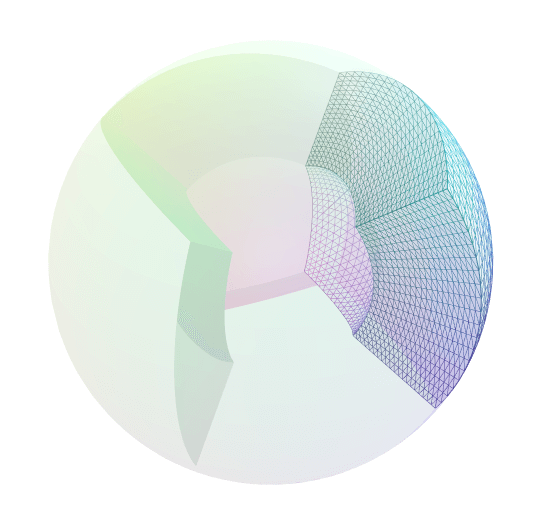
Details

The mapping that goes from a reference cube (in 3D) or square (in 2D) to a wedge centered on a coordinate axis covering a volume between an inner surface and outer surface. Each surface can be given a curvature between flat (a sphericity of 0) or spherical (a sphericity of 1).

In 2D, the first logical coordinate corresponds to the radial coordinate, and the second logical coordinate corresponds to the angular coordinate. In 3D, the first two logical coordinates correspond to the two angular coordinates, and the third to the radial coordinate. This difference originates from separate implementations for the 2D and 3D map that were merged. The 3D implementation can be changed to use the first logical coordinate as the radial direction, but this requires propagating the change through the rest of the domain code (see issue https://github.com/sxs-collaboration/spectre/issues/2988).

The following documentation is for the centered 3D map, as we will defer the dicussion of Wedges with a focal_offset_ to a later section. The 2D map is obtained by setting either of the two angular coordinates to zero (and using \(\xi\) as the radial coordinate). Note that there is also a normalization factor of \(\sqrt{3}\) that appears in multiple expressions in the 3D case that becomes \(\sqrt{2}\) in the 2D case.

The Wedge map is constructed by linearly interpolating between a bulged face of radius radius_inner_ to a bulged face of radius radius_outer_, where the radius of each bulged face is defined to be the radius of the sphere circumscribing the bulge.

We make a choice here as to whether we wish to use the logical coordinates parameterizing these surface as they are, in which case we have the equidistant choice of coordinates, or whether to apply a tangent map to them which leads us to the equiangular choice of coordinates. Wedges have variable opening_angles_ which, for centered Wedges, are the angular sizes of the wedge in the \(\xi\) and \(\eta\) directions (for the 3D case) in the target frame. By default, Wedges have opening angles of \(\pi/2\), so we will discuss that case here and defer both the discussion of generalized opening angles and the interaction between opening angles and non-zero focal offsets for later sections.

For a Wedge with \(\xi\) and \(\eta\) opening angles of \(\pi/2\), the equiangular coordinates in terms of the logical coordinates are:

\begin{align} \textrm{equiangular xi} : \Xi(\xi) = \textrm{tan}(\xi\pi/4) \label{eq:equiangular_xi_pi_over_2} \end{align}

\begin{align} \textrm{equiangular eta} : \mathrm{H}(\eta) = \textrm{tan}(\eta\pi/4) \label{eq:equiangular_eta_pi_over_2} \end{align}

With derivatives:

\begin{align} \Xi'(\xi) &= \frac{\pi}{4}(1+\Xi^2) \\ \mathrm{H}'(\eta) &= \frac{\pi}{4}(1+\mathrm{H}^2) \end{align}

The equidistant coordinates are:

\begin{align} \textrm{equidistant xi} : \Xi = \xi \\ \textrm{equidistant eta} : \mathrm{H} = \eta \end{align}

with derivatives:

\begin{align} \Xi'(\xi) &= 1 \\ \mathrm{H}'(\eta) &= 1 \end{align}

We also define the variable \(\rho\), given by:

\begin{align} \textrm{rho} : \rho = \sqrt{1+\Xi^2+\mathrm{H}^2} \end{align}

The Spherical Face Map

The surface map for the spherical face of radius \(R\) lying in the \(+z\) direction in either choice of coordinates is then given by:

\begin{align} \vec{\sigma}_{spherical}: \vec{\xi} \rightarrow \vec{x}(\vec{\xi}) \end{align}

Where

\begin{align} \vec{x}(\xi,\eta) = \begin{bmatrix} x(\xi,\eta) \\ y(\xi,\eta) \\ z(\xi,\eta) \\ \end{bmatrix} = \frac{R}{\rho} \begin{bmatrix} \Xi \\ \mathrm{H} \\ 1 \\ \end{bmatrix} \end{align}

The Bulged Face Map

The bulged surface is itself constructed by linearly interpolating between a cubical face and a spherical face. The surface map for the cubical face of side length \(2L\) lying in the \(+z\) direction is given by:

\begin{align} \vec{\sigma}_{cubical}: \vec{\xi} \rightarrow \vec{x}(\vec{\xi}) \end{align}

Where

\begin{align} \vec{x}(\xi,\eta) = \begin{bmatrix} x(\xi,\eta) \\ y(\xi,\eta) \\ L \\ \end{bmatrix} = L\begin{bmatrix} \Xi \\ \mathrm{H} \\ 1 \\ \end{bmatrix} \end{align}

To construct the bulged map we interpolate between this cubical face map and a spherical face map of radius \(R\), with the interpolation parameter being \(s\), called the sphericity and which ranges from 0 to 1, with 0 corresponding to a flat surface and 1 corresponding to a spherical surface. The surface map for the bulged face lying in the \(+z\) direction is then given by:

\begin{align} \vec{\sigma}_{bulged}(\xi,\eta) = \left\{(1-s)L + \frac{sR}{\rho}\right\} \begin{bmatrix} \Xi \\ \mathrm{H} \\ 1 \\ \end{bmatrix} \end{align}

We constrain \(L\) by demanding that the spherical face circumscribe the cube. With this condition, we have \(L = R/\sqrt3\).

Note

This differs from the choice in SpEC where it is demanded that the surfaces touch at the cube face centers, which leads to \(L = R\).

The Full Volume Map

The final map for the wedge which lies along the \(+z\) axis is obtained by interpolating between the two surfaces with the interpolation parameter being the logical coordinate \(\zeta\). For a wedge whose gridpoints are linearly distributed in the radial direction (radial_distribution_ is domain::CoordinateMaps::Distribution::Linear), this interpolation results in the following map:

\begin{align} \vec{x}(\xi,\eta,\zeta) = \frac{1}{2}\left\{ (1-\zeta)\Big[ (1-s_{inner})\frac{R_{inner}}{\sqrt 3} + s_{inner}\frac{R_{inner}}{\rho} \Big] + (1+\zeta)\Big[ (1-s_{outer})\frac{R_{outer}}{\sqrt 3} + s_{outer}\frac{R_{outer}}{\rho} \Big] \right\} \begin{bmatrix} \Xi \\ \mathrm{H} \\ 1 \\ \end{bmatrix} \end{align}

We will define the variables \(F(\zeta)\) and \(S(\zeta)\), the frustum and sphere factors (in the linear case):

\begin{align} F(\zeta) &= F_0 + F_1\zeta \label{eq:frustum_factor} \\ S(\zeta) &= S_0 + S_1\zeta \label{eq:sphere_factor} \end{align}

Where

\begin{align} F_0 &= \frac{1}{2} \big\{ (1-s_{outer})R_{outer} + (1-s_{inner})R_{inner} \big\} \label{eq:frustum_zero_linear} \\ F_1 &= \partial_{\zeta}F = \frac{1}{2} \big\{ (1-s_{outer})R_{outer} - (1-s_{inner})R_{inner} \big\} \label{eq:frustum_rate_linear} \\ S_0 &= \frac{1}{2} \big\{ s_{outer}R_{outer} + s_{inner}R_{inner} \big\} \label{eq:sphere_zero_linear} \\ S_1 &= \partial_{\zeta}S = \frac{1}{2} \big\{ s_{outer}R_{outer} - s_{inner}R_{inner}\big\} \label{eq:sphere_rate_linear} \end{align}

The map can then be rewritten as:

\begin{align} \vec{x}(\xi,\eta,\zeta) = \left\{ \frac{F(\zeta)}{\sqrt 3} + \frac{S(\zeta)}{\rho} \right\} \begin{bmatrix} \Xi \\ \mathrm{H} \\ 1 \\ \end{bmatrix} \end{align}

The inverse map is given by:

\begin{align} \xi &= \frac{x}{z} \\ \eta &= \frac{y}{z} \\ \zeta &= \frac{z - \left(\frac{F_0}{\sqrt{3}} + \frac{S_0}{\rho}\right)} {\left(\frac{F_1}{\sqrt{3}} + \frac{S_1}{\rho}\right)} \end{align}

We provide some common derivatives:

\begin{align} \partial_{\xi}z &= \frac{-S(\zeta)\Xi\Xi'}{\rho^3} \\ \partial_{\eta}z &= \frac{-S(\zeta)\mathrm{H}\mathrm{H}'}{\rho^3} \\ \partial_{\zeta}z &= \frac{F'}{\sqrt 3} + \frac{S'(\zeta)}{\rho} \end{align}

The Jacobian then is:

\begin{align} J = \begin{bmatrix} \Xi'z + \Xi\partial_{\xi}z & \Xi\partial_{\eta}z & \Xi\partial_{\zeta}z \\ \mathrm{H}\partial_{\xi}z & \mathrm{H}'z + \mathrm{H}\partial_{\eta}z & \mathrm{H}\partial_{\zeta}z \\ \partial_{\xi}z & \partial_{\eta}z & \partial_{\zeta}z \\ \end{bmatrix} \label{eq:jacobian_centered_wedge} \end{align}

A common factor that shows up in the inverse Jacobian is:

\begin{align} T:= \frac{S(\zeta)}{(\partial_{\zeta}z)\rho^3} \end{align}

The inverse Jacobian then is:

\begin{align} J^{-1} = \frac{1}{z}\begin{bmatrix} \Xi'^{-1} & 0 & -\Xi\Xi'^{-1} \\ 0 & \mathrm{H}'^{-1} & -\mathrm{H}\mathrm{H}'^{-1} \\ T\Xi & T\mathrm{H} & T + F(\partial_{\zeta}z)^{-1}/\sqrt 3 \\ \end{bmatrix} \end{align}

Changing the radial distribution of the gridpoints

By default, Wedge linearly distributes its gridpoints in the radial direction. An exponential distribution of gridpoints can be obtained by linearly interpolating in the logarithm of the radius in order to obtain a relatively higher resolution at smaller radii. Since this is a radial rescaling of Wedge, this option is only supported for fully spherical wedges with sphericity_inner_ = sphericity_outer_ = 1.

The linear interpolation done for a logarithmic radial distribution (radial_distribution_ is domain::CoordinateMaps::Distribution::Logarithmic) is:

\begin{align} \ln r = \frac{1-\zeta}{2}\ln R_{inner} + \frac{1+\zeta}{2}\ln R_{outer} \end{align}

The map then is:

\begin{align} \vec{x}(\xi,\eta,\zeta) = \frac{\sqrt{R_{inner}^{1-\zeta}R_{outer}^{1+\zeta}}}{\rho} \begin{bmatrix} \Xi \\ \mathrm{H} \\ 1 \\ \end{bmatrix} \end{align}

We can rewrite this map to take on the same form as the map for the linear radial distribution, where we set

\begin{align} F(\zeta) &= 0 \\ S(\zeta) &= \sqrt{R_{inner}^{1-\zeta}R_{outer}^{1+\zeta}} \\ \end{align}

Which gives us

\begin{align} \vec{x}(\xi,\eta,\zeta) = \frac{S(\zeta)}{\rho} \begin{bmatrix} \Xi \\ \mathrm{H} \\ 1 \\ \end{bmatrix} \end{align}

The Jacobian then is still Eq. ( \(\ref{eq:jacobian_centered_wedge}\)) but where \(F(\zeta)\) and \(S(\zeta)\) are the quantities defined here for the logarithmic distribution.

Alternatively, an inverse radial distribution (radial_distribution_ is domain::CoordinateMaps::Distribution::Inverse) can be chosen where the linear interpolation is:

\begin{align} \frac{1}{r} = \frac{R_\mathrm{inner} + R_\mathrm{outer}} {2 R_\mathrm{inner}R_\mathrm{outer}} + \frac{R_\mathrm{inner} - R_\mathrm{outer}} {2R_\mathrm{inner} R_\mathrm{outer}} \zeta \end{align}

Which can be rewritten as:

\begin{align} \frac{1}{r} = \frac{1-\zeta}{2R_{inner}} + \frac{1+\zeta}{2R_{outer}} \end{align}

The map likewise takes the form:

\begin{align} \vec{x}(\xi,\eta,\zeta) = \frac{S(\zeta)}{\rho} \begin{bmatrix} \Xi \\ \mathrm{H} \\ 1 \\ \end{bmatrix} \end{align}

Where

\begin{align} F(\zeta) &= 0 \\ S(\zeta) &= \frac{2R_{inner}R_{outer}} {(1 + \zeta)R_{inner} + (1 - \zeta)R_{outer}} \end{align}

Again, the Jacobian is still Eq. ( \(\ref{eq:jacobian_centered_wedge}\)) but where \(F(\zeta)\) and \(S(\zeta)\) are the quantities defined here for the inverse distribution.

Changing the opening angles

Consider the following map on \(\xi \in [-1,1]\), which maps this interval onto a parameterized curve that extends one fourth of a circle.

\begin{align} \vec{\Gamma}(\xi) = \frac{R}{\sqrt{1+\xi^2}} \begin{bmatrix} 1 \\ \xi \\ \end{bmatrix}. \label{eq:quarter_circle} \end{align}

It is convenient to compute the polar coordinate \(\theta\) of the mapped point as a function of \(\xi\):

\begin{align} \theta(\xi) = \tan^{-1}\left(\frac{\Gamma_y(\xi)}{\Gamma_x(\xi)}\right). \label{eq:polar_coord} \end{align}

The opening angle of the map is defined to be:

\begin{align} \Delta \theta = \theta(1) - \theta(-1), \label{eq:define_opening_angle} \end{align}

We can see that with \(\xi=\pm 1\), we have \(\Gamma_x = R/\sqrt{2}\) and \(\Gamma_y=\pm R/\sqrt{2}\), giving us \(\theta(1) = \pi/4\) and \(\theta(-1) = -\pi/4\). This wedge has an opening angle \(\pi/2\) radians, as expected.

On the other hand, the following map has an opening angle of \(\theta_O\):

\begin{align} \vec{\Gamma}(\xi) = \frac{R}{\sqrt{1+\tan^2{(\theta_O/2)}\xi^2}} \begin{bmatrix} 1 \\ \tan{(\theta_O/2)}\xi \\ \end{bmatrix}. \end{align}

Let us also consider the generalized map

\begin{align} \vec{\Gamma}(\xi) = \frac{R}{\sqrt{1+\Xi^2}} \begin{bmatrix} 1 \\ \Xi \\ \end{bmatrix}, \end{align}

where \(\Xi(\xi)\) is a function of \(\xi\). \(\theta(\xi)\) can then be written as

\begin{align} \theta(\xi) = \tan^{-1}(\Xi). \label{eq:theta} \end{align}

For the map \(\Xi(\xi) = \tan(\pi\xi/4)\), Eq. ( \(\ref{eq:theta}\)) yields \(\theta(\xi) = \pi\xi/4\) and \(\Delta\theta = \pi/2\). Note that this choice of \(\Xi(\xi)\) is equivalent to a reparameterization of the previous map given in Eq. ( \(\ref{eq:quarter_circle}\)). The reparameterization of the curve \(\vec{\Gamma}(\xi)\) via the tangent map yields an empirically superior gridpoint distribution in practice. That this reparameterization should have this property can be motivated by an observation of the following:

\begin{align} \frac{\mathrm{d}\tan^{-1}\Xi}{\mathrm{d}\xi} = \frac{1}{1+\Xi^2}\frac{\mathrm{d}\Xi}{\mathrm{d}\xi} = \frac{\pi}{4}. \end{align}

In other words, this parameterization has the property that the logical coordinate \(\xi\) subtends the angle \(\theta\) at a constant rate. In general, we say that a curve \(\vec{\Gamma}(\xi)\) is parameterized equiangularly if

\begin{align} \frac{\mathrm{d}\theta}{\mathrm{d}\xi} = \text{const}. \end{align}

As for the map

\begin{align} \Xi(\xi) = \tan{(\theta_O/2)}\frac{\tan{(\theta_D \xi/2)}}{\tan{(\theta_D/2)}}, \end{align}

this choice of \(\Xi(\xi)\) results in a \(\vec{\Gamma}(\xi)\) with opening angle \(\theta_O\), which is equiangularly distributed if \(\theta_O = \theta_D\). In the Wedge map, the argument with_adapted_equiangular_map controls whether to set \(\theta_O = \theta_D\) (the true case) or to set \(\theta_D = \pi/2\) (the false case). When working with a 3D Wedge, the opening angles for the Wedge can be separately controlled for both the \(\xi\) and \(\eta\) directions, but with_adapted_equiangular_map will apply to both directions. Additionally in the 3D case, it is not possible to set with_equiangular_map_ to true for all of the six wedges of a sphere unless every opening angle is \(\pi/2\). In the BinaryCompactObject domain, the outer \(+y\), \(-y\), \(+z\), and \(-z\) Wedges are allowed to have a user-specified opening angle in the \(\xi\)-direction, with a corresponding \(\theta_D\) equal to this opening angle, while in the \(\eta\)-direction the opening angle is set to \(\pi/2\). The two end cap Wedges in the \(+x\) and \(-x\) directions have angular dimensions and gridpoint distributions determined by the other four Wedges, as the six Wedges must conforming have gridpoint distributions at the \(\xi = \pm1\), \(\eta = \pm 1\) boundaries.

Wedge with a Focal Offset

Wedges without and with a focal offset

In the case of the rectangular BinaryCompactObject domain, it becomes desirable to offset the center of the spherical excision surface relative to the center of the cubical surface surrounding it. To enable the offsetting of the central excision, the Wedge map must be generalized according to the focal lifting method, which we will now discuss.

We consider the problem of creating parameterized volumes from parameterized surfaces. Consider a parameterized surface \(\vec{\sigma}_{parent}(\xi,\eta)\), also referred to as the parent surface. We define focal lifting as the projection of this parent surface into a three-dimensional parameterized volume \(\vec{x}(\xi,\eta, \zeta)\) with respect to some focus \(\vec{x}_0\) and lifting scale factor \(\Lambda(\xi,\eta,\zeta)\). The resulting volume is then said to be a focally lifted volume. These volume maps can be cast into the following form:

\begin{align} \vec{x} - \vec{x}_0 = \Lambda(\vec{\sigma}_{parent}-\vec{x}_0), \label{eq:focal_lifting} \end{align}

which makes apparent how the mapped point \(\vec{x}(\xi,\eta,\zeta)\) is obtained. The parametric equations for the generalized 3D Wedge maps can all be written in the above form, which we will refer to as focally lifted form. In the case of the 3D Wedge map with no focal offset, we have:

\begin{align} \vec{x}_0 &= 0 \\ \Lambda &= \left\{\frac{F(\zeta)}{\sqrt{3}} + \frac{S(\zeta)}{\rho} \right\} \\ \vec{\sigma}_{parent} &= \begin{bmatrix} \Xi, \mathrm{H}, 1 \end{bmatrix}^T \end{align}

The above map can be thought of as constructing a wedge from a biunit cube centered at the origin. Points on the parent surface are scaled by a factor of \(\Lambda(\xi,\eta,\zeta)\) to obtain the corresponding point in the volume. When generalizing the map to have a focus shifted from the origin (obtained by setting focal_offset_ to be non-zero), we scale the original parent surface \(\vec{\sigma}_{parent} = [\Xi, \mathrm{H},1]^T\) by a factor \(L\), and let the focus \(\vec{x_0}\) shift away from the origin. The generalized wedge map is then given by:

\begin{align} \vec{x} - \vec{x}_0 = \left\{\frac{F(\zeta)}{L\sqrt 3} + \frac{S(\zeta)}{L\rho}\right\} \begin{bmatrix} L\Xi - x_0 \\ L\mathrm{H} - y_0 \\ L-z_0 \\ \end{bmatrix} \end{align}

where we are now defining \(\rho\) to be

\begin{align} \rho = \sqrt{(\Xi - x_0/L)^2 + (\mathrm{H} - y_0/L)^2 + (1 - z_0/L)^2}. \label{eq:generalized_rho} \end{align}

This map is often written as:

\begin{align} \vec{x} - \vec{x}_0 = \left\{\frac{F(\zeta)}{\sqrt{3}} + \frac{S(\zeta)}{\rho}\right\}(\vec{\sigma}_0 - \vec{x}_0/L), \label{eq:focally_lifted_map_with_s_and_f_factors} \end{align}

where \(\vec{\sigma}_0 = [\Xi, \mathrm{H},1]^T\), as the parent surface \(\vec{\sigma}_{parent}\) is now \(L\vec{\sigma}_0\). We give the quantity in braces the name \(z_{\Lambda} = L\Lambda\), generalized z. With this definition, we can rewrite Eq. ( \(\ref{eq:focally_lifted_map_with_s_and_f_factors}\)) in the simpler form,

\begin{align} \vec{x} - \vec{x}_0 = z_{\Lambda}(\vec{\sigma}_0 - \vec{x}_0/L). \label{eq:focally_lifted_map_with_generalized_z_coef} \end{align}

Note

In the offset case, the frustum factor \(F(\zeta)\) and sphere factor \(S(\zeta)\) (Eqs. ( \(\ref{eq:frustum_factor}\)) and ( \(\ref{eq:sphere_factor}\))) for a linear radial distribution are no longer defined by the general \(F_0\), \(F_1\), \(S_0\), and \(S_1\) given by Eqs. ( \(\ref{eq:frustum_zero_linear}\)), ( \(\ref{eq:frustum_rate_linear}\)), ( \(\ref{eq:sphere_zero_linear}\)), and ( \(\ref{eq:sphere_rate_linear}\)). In the offset case, the inner surface must be spherical \((s_{inner} = 1)\) and the outer surface can only be spherical or flat \((s_{outer} = 0 \textrm{ or } s_{outer} = 1)\). In the case where \(s_{outer} = 0\), \(L/\sqrt{3}\) is taken to be \(R_{outer}\).

The map can be inverted by first solving for \(z_{\Lambda}\) in terms of the target coordinates. We make use of the fact that the parent surface \(\vec{\sigma}_{parent}\) has a constant normal vector \(\hat{n} = \hat{z}\).

\begin{align} z_{\Lambda} = \frac{(\vec{x} - \vec{x}_0)\cdot\hat{n}} {(\vec{\sigma}_0-\vec{x}_0/L)\cdot\hat{n}}. \end{align}

In other words, when \(\hat{n} = \hat{z}\),

\begin{align} z_{\Lambda} = \left\{\frac{F(\zeta)}{\sqrt{3}} + \frac{S(\zeta)}{\rho}\right\} = \frac{z - z_0}{1 - z_0/L} \end{align}

Moving all the known quantities in Eq. ( \(\ref{eq:focally_lifted_map_with_generalized_z_coef}\)) to the left hand side results in the following expression that solves for the source coordinates \(\xi\) and \(\eta\) in terms of the target coordinates:

\begin{align} \frac{\vec{x} - \vec{x}_0}{z_{\Lambda}} + \frac{\vec{x}_0}{L} = \vec{\sigma}_0(\xi,\eta) = \begin{bmatrix} \Xi \\ \mathrm{H} \\ 1 \\ \end{bmatrix}, \end{align}

Note that \(|\vec{\sigma}_0 - \vec{x}_0/L| = \sqrt{(\Xi - x_0/L)^2 + (\mathrm{H} - y_0/L)^2 + (1 - z_0/L)^2} = \rho\), indicating that an expression for \(\rho\) in terms of the target coordinates can be computed via taking the magnitude of both sides of Eq. ( \(\ref{eq:focally_lifted_map_with_generalized_z_coef}\)):

\begin{align} |\vec{x} - \vec{x}_0| = z_{\Lambda}|\vec{\sigma}_0 - \vec{x}_0/L| = z_{\Lambda}\rho. \end{align}

The quantity \(\rho\) is then given by:

\begin{align} \rho = \frac{|\vec{x} - \vec{x}_0|}{z_{\Lambda}}. \end{align}

With \(\rho\) computed, the radial source coordinate \(\zeta\) can be computed from

\begin{align} z_{\Lambda} = \left\{\frac{F(\zeta)}{\sqrt{3}} + \frac{S(\zeta)}{\rho} \right\} = \left\{\frac{F_0}{\sqrt{3}} + \frac{S_0}{\rho} + \frac{F_1\zeta}{\sqrt{3}} + \frac{S_1\zeta}{\rho}\right\}, \end{align}

which gives

\begin{align} \zeta = \frac{z_{\Lambda} - \left(\frac{F_0}{\sqrt{3}} + \frac{S_0}{\rho}\right)} {\left(\frac{F_1}{\sqrt{3}} + \frac{S_1}{\rho}\right)}. \end{align}

To compute the Jacobian, it is useful to first note that \(\rho\) (Eq. ( \(\ref{eq:generalized_rho}\))) is the magnitude of the vector

\begin{align} \vec{\rho} = \vec{\sigma}_0 - \vec{x}_0/L = \begin{bmatrix} \Xi - x_0/L \\ \mathrm{H} - y_0/L \\ 1 - z_0/L \end{bmatrix} \end{align}

and that we can express the target coordinates in Eq. ( \(\ref{eq:focally_lifted_map_with_generalized_z_coef}\)) in terms of the components of \(\vec{\rho}\):

\begin{align} x &= z_{\Lambda}\rho_x + x_0 \\ y &= z_{\Lambda}\rho_y + y_0 \\ z &= z_{\Lambda}\rho_z + z_0 \end{align}

Some common terms used in the Jacobian are the derivatives of \(z_{\Lambda}\) with respect to the source coordinates:

\begin{align} \partial_{\xi}z_{\Lambda} &= \frac{-S(\zeta)\Xi'\rho_x}{\rho^3} \\ \partial_{\eta}z_{\Lambda} &= \frac{-S(\zeta)\mathrm{H}'\rho_y}{\rho^3} \\ \partial_{\zeta}z_{\Lambda} &= \frac{F'(\zeta)}{\sqrt{3}} + \frac{S'(\zeta)}{\rho} \end{align}

The Jacobian then is:

\begin{align} J = \begin{bmatrix} \Xi'z_{\Lambda} + \rho_x\partial_{\xi}z_{\Lambda} & \rho_x\partial_{\eta}z_{\Lambda} & \rho_x\partial_{\zeta}z_{\Lambda} \\ \rho_y\partial_{\xi}z_{\Lambda} & \mathrm{H}'z_{\Lambda} + \rho_y\partial_{\eta}z_{\Lambda} & \rho_y\partial_{\zeta}z_{\Lambda} \\ \rho_z\partial_{\xi}z_{\Lambda} & \rho_z\partial_{\eta}z_{\Lambda} & \rho_z\partial_{\zeta}z_{\Lambda} \\ \end{bmatrix} \end{align}

A common factor that shows up in this inverse Jacobian is:

\begin{align} T:= \frac{S(\zeta)}{(\partial_{\zeta}z_{\Lambda})\rho^3} \end{align}

And the inverse Jacobian is then:

\begin{align} J^{-1} = \frac{1}{z_{\Lambda}}\begin{bmatrix} \Xi'^{-1} & 0 & -\rho_x(\Xi'\rho_z)^{-1} \\ 0 & \mathrm{H}'^{-1} & -\rho_y(\mathrm{H}'\rho_z)^{-1} \\ T\rho_x & T\rho_y & T\rho_z + F(\partial_{\zeta}z_{\Lambda}\rho_z)^{-1}/\sqrt{3} \end{bmatrix} \end{align}

Offsetting a Rotated Wedge

The default Wedge map is oriented in the \(+z\) direction, so the construction of a Wedge oriented along a different direction requires an additional OrientationMap \(R\) to be passed to orientation_of_wedge. When offsetting a rotated Wedge, the coordinates passed as parameters to focal_offset are in the coordinate frame in which the Wedge is rotated (the target frame). However, the focal lifting procedure (shown in Eq. ( \(\ref{eq:focal_lifting}\))) is done in the default frame in which the Wedge is facing the \(+z\) direction, so the focal offset \(\vec{x}_0\) is first hit by the inverse rotation \(R^{-1}\) and then the rotated focus \(R^{-1}\vec{x}_0\) is used internally as the focus for the \(+z\) Wedge. When the focal lifting calculation has completed, the rotation of the \(+z\) Wedge into the desired orientation by \(R\) also rotates the focus into the desired location. When performing the inverse operation, the focus is similarly rotated into the default frame, where the inversion is performed.

Interaction between opening angles and focal offsets

When a Wedge is created with a non-zero focal offset, the resulting shape can take on a variety of possible angular sizes, depending on where the focus is placed relative to the default centered location. The reader might note that the angular size of a Wedge can also be controlled by passing an argument to the opening_angles parameter in the Wedge constructor. While both of these methods allow the angular size of a Wedge to be changed, the user is prevented from employing both of them at the same time. In particular, when the the offset is set to some non-zero value, the opening_angles_ member variable is set to \(\pi/2\). Note that the opening_angles_ member being set to \(\pi/2\) does not imply the resulting Wedge will have an angular size of \(\pi/2\). On the contrary, the Wedge will have the angular size that is determined by the application of the focal lifting method on the parent surface, which is the upper \(+z\) face of a cube that is centered at the origin.

Because opening_angles_ is set to \(\pi/2\) when there is a non-zero focal offset, when there is a non-zero focal offset and with_equiangular_map_ is true, \(\Xi\) is given by Eq. ( \(\ref{eq:equiangular_xi_pi_over_2}\)) and \(\mathrm{H}\) by Eq. ( \(\ref{eq:equiangular_eta_pi_over_2}\)), just as it is for the case of a centered Wedge with opening_angles_ of \(\pi/2\).

Member Enumeration Documentation

WedgeHalves

template<size_t Dim>

enum class domain::CoordinateMaps::Wedge::WedgeHalves

strong

Enumerator
Both	Use the entire wedge.
UpperOnly	Use only the upper logical half.
LowerOnly	Use only the lower logical half.

Constructor & Destructor Documentation

Wedge() [1/2]

template<size_t Dim>

domain::CoordinateMaps::Wedge< Dim >::Wedge	(	double	radius_inner,
		double	radius_outer,
		double	sphericity_inner,
		double	sphericity_outer,
		OrientationMap< Dim >	orientation_of_wedge,
		bool	with_equiangular_map,
		WedgeHalves	halves_to_use = WedgeHalves::Both,
		Distribution	radial_distribution = Distribution::Linear,
		const std::array< double, Dim - 1 > &	opening_angles = make_array< Dim - 1 >(M_PI_2),
		bool	with_adapted_equiangular_map = true
	)

Constructs a centered wedge (one with no focal offset)

Parameters

radius_inner	Distance from the origin to one of the corners which lie on the inner surface.
radius_outer	Distance from the origin to one of the corners which lie on the outer surface.
orientation_of_wedge	The orientation of the desired wedge relative to the orientation of the default wedge which is a wedge that has its curved surfaces pierced by the upper-z axis. The logical \(\xi\) and \(\eta\) coordinates point in the cartesian x and y directions, respectively.
sphericity_inner	Value between 0 and 1 which determines whether the inner surface is flat (value of 0), spherical (value of 1) or somewhere in between.
sphericity_outer	Value between 0 and 1 which determines whether the outer surface is flat (value of 0), spherical (value of 1) or somewhere in between.
with_equiangular_map	Determines whether to apply a tangent function mapping to the logical coordinates (for true) or not (for false).
halves_to_use	Determines whether to construct a full wedge or only half a wedge. If constructing only half a wedge, the resulting shape has a face normal to the x direction (assuming default OrientationMap). If constructing half a wedge, an intermediate affine map is applied to the logical xi coordinate such that the interval [-1,1] is mapped to the corresponding logical half of the wedge. For example, if UpperOnly is specified, [-1,1] is mapped to [0,1], and if LowerOnly is specified, [-1,1] is mapped to [-1,0]. The case of Both means a full wedge, with no intermediate map applied. In all cases, the logical points returned by the inverse map will lie in the range [-1,1] in each dimension. Half wedges are currently only useful in constructing domains for binary systems.
radial_distribution	Determines how to distribute gridpoints along the radial direction. For wedges that are not exactly spherical, only Distribution::Linear is currently supported.
opening_angles	Determines the angular size of the wedge. The default value is \(\pi/2\), which corresponds to a wedge size of \(\pi/2\). For this setting, four Wedges can be put together to cover \(2\pi\) in angle along a great circle. This option is meant to be used with the equiangular map option turned on.
with_adapted_equiangular_map	Determines whether to adapt the point distribution in the wedge to match its physical angular size. When true, angular distances are proportional to logical distances. Note that it is not possible to use adapted maps in every Wedge of a Sphere unless each Wedge has the same size along both angular directions.

Wedge() [2/2]

template<size_t Dim>

domain::CoordinateMaps::Wedge< Dim >::Wedge	(	double	radius_inner,
		std::optional< double >	radius_outer,
		double	cube_half_length,
		std::array< double, Dim >	focal_offset,
		OrientationMap< Dim >	orientation_of_wedge,
		bool	with_equiangular_map,
		WedgeHalves	halves_to_use = WedgeHalves::Both,
		Distribution	radial_distribution = Distribution::Linear
	)

Constructs a wedge with a focal offset.

Details

Can construct an offset Wedge with a spherical inner surface and either a spherical or a flat outer surface. If radius_outer has a value, a spherical Wedge will be constructed, and if not, a flat one will be constructed.

Note that because the focal offset is what determines the angular size of the Wedge, opening angles cannot be used with offset Wedges.

In the event that focal_offset happens to be zero, the Wedge's member variables and behavior will be set up to be equivalent to that of a centered Wedge:

• cube_half_length will be ignored
• if radius_outer is std::nullopt, the outer radius of the Wedge will be set to \(\sqrt{\mathrm{Dim}}L\), where \(L\) is the cube_half_length
• the opening angles ( \(\theta_O\)) and opening angles distribution ( \(\theta_D\)) used will be \(\pi/2\)

Parameters

radius_inner	Distance from the origin to one of the corners which lie on the inner surface.
radius_outer	If this has a value, it creates a spherical Wedge (inner and outer sphericity are 1) where this is the distance from the origin to one of the corners that lie on the inner surface. If this is std::nullopt, it creates a Wedge with a flat outer surface (inner sphericity is 1 and outer sphericity is 0). In the event that radius_outer == std::nullopt and focal_offset is zero, the outer radius will instead be set to \(\sqrt{\mathrm{Dim}}L\), where \(L\) is the cube_half_length. The outer radius is given a value in this circumstance so that it can be handled as a centered Wedge (one with no offset).
orientation_of_wedge	The orientation of the desired wedge relative to the orientation of the default wedge which is a wedge that has its curved surfaces pierced by the upper-z axis. The logical \(\xi\) and \(\eta\) coordinates point in the cartesian x and y directions, respectively.
cube_half_length	Half the length of the parent surface (see Wedge documentation for more details). If focal_offset is zero, this parameter has no effect and is ignored so that the Wedge can be handled as a centered Wedge (one with no offset).
focal_offset	The target frame coordinates of the focus from which the Wedge is focally lifted.
with_equiangular_map	Determines whether to apply a tangent function mapping to the logical coordinates (for true) or not (for false).
halves_to_use	Determines whether to construct a full wedge or only half a wedge. If constructing only half a wedge, the resulting shape has a face normal to the x direction (assuming default OrientationMap). If constructing half a wedge, an intermediate affine map is applied to the logical xi coordinate such that the interval [-1,1] is mapped to the corresponding logical half of the wedge. For example, if UpperOnly is specified, [-1,1] is mapped to [0,1], and if LowerOnly is specified, [-1,1] is mapped to [-1,0]. The case of Both means a full wedge, with no intermediate map applied. In all cases, the logical points returned by the inverse map will lie in the range [-1,1] in each dimension. Half wedges are currently only useful in constructing domains for binary systems.
radial_distribution	Determines how to distribute gridpoints along the radial direction. For wedges that are not exactly spherical, only Distribution::Linear is currently supported.

---

The documentation for this class was generated from the following file:

• src/Domain/CoordinateMaps/Wedge.hpp