domain::CoordinateMaps::Frustum Class Reference

A reorientable map from the cube to a frustum. More...

#include <Frustum.hpp>

Public Member Functions
	Frustum (const std::array< std::array< double, 2 >, 4 > &face_vertices, double lower_bound, double upper_bound, OrientationMap< 3 > orientation_of_frustum, bool equiangular_map_at_outer=false, bool equiangular_map_at_inner=false, Distribution zeta_distribution=Distribution::Linear, std::optional< double > distribution_value=std::nullopt, double sphericity=0.0, double transition_phi=0.0, double opening_angle=M_PI_2)
	Frustum (Frustum &&)=default
	Frustum (const Frustum &)=default
Frustum &	operator= (const Frustum &)=default
Frustum &	operator= (Frustum &&)=default
template<typename T >
std::array< tt::remove_cvref_wrap_t< T >, 3 >	operator() (const std::array< T, 3 > &source_coords) const
std::optional< std::array< double, 3 > >	inverse (const std::array< double, 3 > &target_coords) const
	Returns std::nullopt if \(z\) is at or beyond the \(z\)-coordinate of the apex of the pyramid, tetrahedron, or triangular prism that is formed by extending the Frustum (for a \(z\)-oriented Frustum). The inverse function is only callable with doubles because the inverse might fail if called for a point out of range, and it is unclear what should happen if the inverse were to succeed for some points in a DataVector but fail for other points.
template<typename T >
tnsr::Ij< tt::remove_cvref_wrap_t< T >, 3, Frame::NoFrame >	jacobian (const std::array< T, 3 > &source_coords) const
template<typename T >
tnsr::Ij< tt::remove_cvref_wrap_t< T >, 3, Frame::NoFrame >	inv_jacobian (const std::array< T, 3 > &source_coords) const
void	pup (PUP::er &p)
bool	is_identity () const

Static Public Attributes
static constexpr size_t	dim = 3

Friends
bool	operator== (const Frustum &lhs, const Frustum &rhs)

Detailed Description

A reorientable map from the cube to a frustum.

A frustum with rectangular bases.

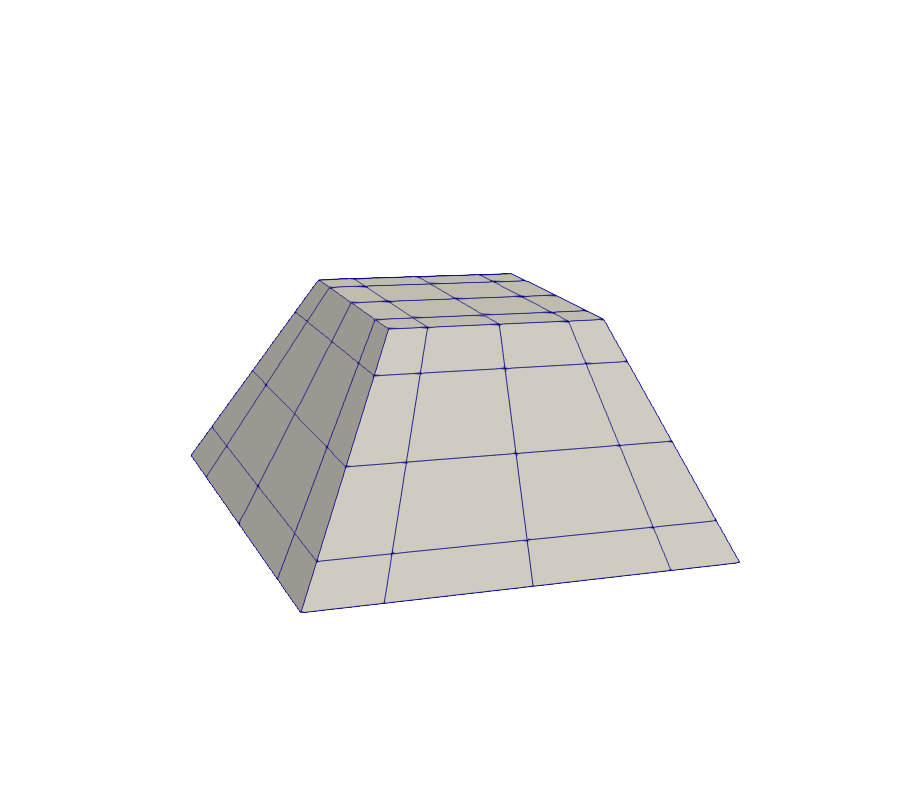
Description and Specifiable Parameters

A map from the logical cube to the volume determined by interpolating between two parallel rectangles each perpendicular to the \(z\)-axis. A Frustum map \(\vec{x}(\xi,\eta,\zeta)\) is determined by specifying two heights \(z_1 = \) lower_bound and \(z_2 = \) upper_bound for the positions of the rectangular bases of the frustum along the \(z-\)axis, and the sizes of the rectangles are determined by the eight values passed to face_vertices:

\begin{align*} &\textrm{lower x upper base} : x^{+\zeta}_{-\xi,-\eta} = x(-1,-1,1)\\ &\textrm{lower x lower base} : x^{-\zeta}_{-\xi,-\eta} = x(-1,-1,-1)\\ &\textrm{upper x upper base} : x^{+\zeta}_{+\xi,+\eta} = x(1,1,1)\\ &\textrm{upper x lower base} : x^{-\zeta}_{+\xi,+\eta} = x(1,1,-1)\\ &\textrm{lower y upper base} : y^{+\zeta}_{-\xi,-\eta} = y(-1,-1,1)\\ &\textrm{lower y lower base} : y^{-\zeta}_{-\xi,-\eta} = y(-1,-1,-1)\\ &\textrm{upper y upper base} : y^{+\zeta}_{+\xi,+\eta} = y(1,1,1)\\ &\textrm{upper y lower base} : y^{-\zeta}_{+\xi,+\eta} = y(1,1,-1)\end{align*}

Note

As an example, consider a frustum along the z-axis, with the lower base starting at (x,y) = (-2.0,3.0) and extending to (2.0,5.0), and with the upper base extending from (0.0,1.0) to (1.0,3.0). The corresponding value for face_vertices is {{{{-2.0,3.0}}, {{2.0,5.0}}, {{0.0,1.0}}, {{1.0,3.0}}}}.

In the case where the two rectangles are geometrically similar, the volume formed is a geometric frustum. However, this coordinate map generalizes to rectangles which need not be similar. The user may reorient the frustum by passing an OrientationMap to the constructor. If with_equiangular_map is true, then this coordinate map applies a tangent function mapping to the logical \(\xi\) and \(\eta\) coordinates. We then refer to the generalized logical coordinates as \(\Xi\) and \(\mathrm{H}\). If projective_scale_factor is set to a quantity other than unity, then this coordinate map applies a rational function mapping to the logical \(\zeta\) coordinate. This generalized logical coordinate is referred to as \(\mathrm{Z}\). If auto_projective_scale_factor is true, the user-specified projective_scale_factor is ignored and an appropriate value for projective_scale_factor is computed based on the values passed to face_vertices. See the page on redistributing gridpoints to see more detailed information on equiangular variables and projective scaling.

Coordinate Map and Jacobian

In terms of the face_vertices variables, we define the following auxiliary variables:

\begin{align*}\Sigma^x &= \frac{1}{4}(x^{+\zeta}_{-\xi,-\eta} + x^{+\zeta}_{+\xi,+\eta} + x^{-\zeta}_{-\xi,-\eta} + x^{-\zeta}_{+\xi,+\eta}) \\ \Delta^x_{\zeta} &= \frac{1}{4}(x^{+\zeta}_{-\xi,-\eta} + x^{+\zeta}_{+\xi,+\eta} - x^{-\zeta}_{-\xi,-\eta} - x^{-\zeta}_{+\xi,+\eta}) \\ \Delta^x_{\xi} &= \frac{1}{4}(x^{+\zeta}_{+\xi,+\eta} - x^{+\zeta}_{-\xi,-\eta} + x^{-\zeta}_{+\xi,+\eta} - x^{-\zeta}_{-\xi,-\eta}) \\ \Delta^x_{\xi\zeta} &= \frac{1}{4}(x^{+\zeta}_{+\xi,+\eta} - x^{+\zeta}_{-\xi,-\eta} - x^{-\zeta}_{+\xi,+\eta} + x^{-\zeta}_{-\xi,-\eta}) \\ \Sigma^y &= \frac{1}{4}(y^{+\zeta}_{-\xi,-\eta} + y^{+\zeta}_{+\xi,+\eta} + y^{-\zeta}_{-\xi,-\eta} + y^{-\zeta}_{+\xi,+\eta}) \\ \Delta^y_{\zeta} &= \frac{1}{4}(y^{+\zeta}_{-\xi,-\eta} + y^{+\zeta}_{+\xi,+\eta} - y^{-\zeta}_{-\xi,-\eta} - y^{-\zeta}_{+\xi,+\eta}) \\ \Delta^y_{\eta} &= \frac{1}{4}(y^{+\zeta}_{+\xi,+\eta} - y^{+\zeta}_{-\xi,-\eta} + y^{-\zeta}_{+\xi,+\eta} - y^{-\zeta}_{-\xi,-\eta}) \\ \Delta^y_{\eta\zeta} &= \frac{1}{4}(y^{+\zeta}_{+\xi,+\eta} - y^{+\zeta}_{-\xi,-\eta} - y^{-\zeta}_{+\xi,+\eta} + y^{-\zeta}_{-\xi,-\eta}) \\ \Sigma^z &= \frac{z_1 + z_2}{2}\\ \Delta^z &= \frac{z_2 - z_1}{2} \end{align*}

The full map is then given by:

\[\vec{x}(\xi,\eta,\zeta) = \begin{bmatrix} \Sigma^x + \Delta^x_{\xi}\Xi + (\Delta^x_{\zeta} + \Delta^x_{\xi\zeta}\Xi)\mathrm{Z}\\ \Sigma^y + \Delta^y_{\eta}\mathrm{H} + (\Delta^y_{\zeta} + \Delta^y_{\eta\zeta}\mathrm{H})\mathrm{Z}\\ \Sigma^z + \Delta^z\mathrm{Z}\\ \end{bmatrix}\]

With Jacobian:

\[J = \begin{bmatrix} (\Delta^x_{\xi} + \Delta^x_{\xi\zeta}\mathrm{Z})\Xi' & 0 & (\Delta^x_{\zeta}+ \Delta^x_{\xi\zeta}\Xi)\mathrm{Z}' \\ 0 & (\Delta^y_{\eta} + \Delta^y_{\eta\zeta}\mathrm{Z})\mathrm{H}' & (\Delta^y_{\zeta} + \Delta^y_{\eta\zeta}\mathrm{H})\mathrm{Z}'\\ 0 & 0 & \Delta^z\mathrm{Z}' \\ \end{bmatrix} \]

Suggested values for the projective scale factor

Note

This section assumes familiarity with projective scaling as discussed on the page on redistributing gridpoints.

When constructing a Frustum map, it is not immediately obvious what value of \(w_{\delta}\) to use in the projective map; here we present a choice of \(w_{\delta}\) that will produce minimal grid distortion. We cover two cases: the first is the special case in which the two rectangular Frustum bases are related by a simple scale factor; the second is the general case.

Trapezoids from squares. (Davide Cervone)

As seen in Cervone's [Cubes and Hypercubes Rotating] (http://www.math.union.edu/~dpvc/math/4D/rotation/welcome.html), there is a special case in which the inverse projection of a trapezoid is not another trapezoid, but a rectangle where the bases are congruent. Most often one will want to use the special value of \(w_{\delta}\) where this occurs. This value of \(w_{\delta}\) corresponds to the projective transformation mapping a rectangular prism in an ambient 4D space with congruent faces at \(w=1\) and \(w=w_{\delta}\) to the frustum in the plane \(w=1\):

\[w_{\delta} = \frac{L_1}{L_2}\]

where \(\frac{L_1}{L_2}\) is the ratio between any pair of corresponding side lengths of the \(z_1\) and \(z_2\)-bases of the frustum, respectively.

For the general case one will want to use the value:

\[w_{\delta} = \frac{\sqrt{(x^{-\zeta}_{+\xi,+\eta} - x^{-\zeta}_{-\xi,+\eta}) (y^{-\zeta}_{+\xi,+\eta} - y^{-\zeta}_{+\xi,-\eta})}} {\sqrt{(x^{+\zeta}_{+\xi,+\eta} - x^{+\zeta}_{-\xi,+\eta}) (y^{+\zeta}_{+\xi,+\eta} - y^{+\zeta}_{+\xi,-\eta})}}\]

This is the value for \(w_{\delta}\) used by this CoordinateMap when auto_projective_scale_factor is true.

Bulged Frustum Coordinate Map and Jacobian

Each of the frustum faces in the frustum map given above are flat, but the upper +z face of the frustum can be bulged out by setting a non-zero value for the sphericity, where a value of 0.0 corresponds to the usual flat- face, and a value of 1.0 corresponds to a value of fully spherical. Using OrientationMaps allows the user to create a set of frustums that fully cover a spherical surface. The radius of the sphere is determined by the corner of the frustum that is furthest from the origin.

The full map is given by:

\[\vec{x}(\xi,\eta,\zeta) = \begin{bmatrix} \Sigma^x + \Delta^x_{\xi}\Xi + (\Delta^x_{\zeta} + \Delta^x_{\xi\zeta}\Xi)\mathrm{Z}\\ \Sigma^y + \Delta^y_{\eta}\mathrm{H} + (\Delta^y_{\zeta} + \Delta^y_{\eta\zeta}\mathrm{H})\mathrm{Z}\\ \Sigma^z + \Delta^z\mathrm{Z}\\ \end{bmatrix} + s \frac{1 + \mathrm{Z}}{2}\left(\frac{R}{|\vec{\sigma}_{\mathrm{+z}}|}-1\right) \vec{\sigma}_{\mathrm{+z}} \]

where \(R\) is the radius, \(s\) is the sphericity, and \(\vec{\sigma}_{\mathrm{+z}}\) is given by:

\[ \vec{\sigma}_{\mathrm{+z}} = \begin{bmatrix} \Sigma^x + \Delta^x_{\xi}\Xi + \Delta^x_{\zeta} + \Delta^x_{\xi\zeta}\Xi\\ \Sigma^y + \Delta^y_{\eta}\mathrm{H} + \Delta^y_{\zeta} + \Delta^y_{\eta\zeta}\mathrm{H}\\ \Sigma^z + \Delta^z\\ \end{bmatrix}. \]

The Jacobian is:

\[J = \begin{bmatrix} (\Delta^x_{\xi} + \Delta^x_{\xi\zeta}\mathrm{Z})\Xi' & 0 & (\Delta^x_{\zeta}+ \Delta^x_{\xi\zeta}\Xi)\mathrm{Z}' \\ 0 & (\Delta^y_{\eta} + \Delta^y_{\eta\zeta}\mathrm{Z})\mathrm{H}' & (\Delta^y_{\zeta} + \Delta^y_{\eta\zeta}\mathrm{H})\mathrm{Z}'\\ 0 & 0 & \Delta^z\mathrm{Z}' \\ \end{bmatrix} + \frac{s}{2} \left\{ \left(\frac{R}{|\vec{\sigma}_{\mathrm{+z}}|}-1\right) \vec{\sigma}_{\mathrm{+z}}\hat{\zeta}^{\intercal}\mathrm{Z}'+ (1+\mathrm{Z})\left(\frac{R}{|\vec{\sigma}_{\mathrm{+z}}|}\left( \mathbb{1}-\frac{\vec{\sigma}_{\mathrm{+z}} \vec{\sigma}_{\mathrm{+z}}^{\intercal}} {|\vec{\sigma}_{\mathrm{+z}}|^2}\right)-\mathbb{1}\right) J_{\sigma}\right\}, \]

where \(\hat{\zeta}\) is the row vector \([0, 0, 1]\), and \(J_{\sigma}\) is the Jacobian of the upper +z surface, given by:

\[ J_{\sigma} = \begin{bmatrix} (\Delta^x_{\xi} + \Delta^x_{\xi\zeta})\Xi' & 0 & 0 \\ 0 & (\Delta^y_{\eta} + \Delta^y_{\eta\zeta})\mathrm{H}' & 0 \\ 0 & 0 & 0 \\ \end{bmatrix}. \]

Using the Frustum Transition between Equiangular Maps

Using the parameter \(\phi\), the user can specify whether to use the full equiangular map on the upper +z face, or whether to use only the upper or lower half of the equiangular map on the upper +z face. This capability is used in the BinaryCompactObject Domain, where two equiangular maps around each spherical object must be transitioned into a single equiangular map at the outer boundary. The transition region that interpolates between these two regions is the layer of Blocks with the Frustum maps.

The full map is obtained by setting \(\Xi = \frac{1 + \mathrm{Z}}{2}\Xi_{\mathrm{upper}}(\xi,\zeta) + \frac{1 - \mathrm{Z}}{2}\Xi_{0}(\xi)\)

for the volume map \(\vec{x}(\xi,\eta,\zeta)\), and \(\Xi = \Xi_{\mathrm{upper}}\) for the surface map \(\vec{\sigma}(\xi,\eta)\), where \(\Xi_{\mathrm{upper}}\) is the \(\phi\)-dependent generalized equiangular map, which corresponds to the lower half of the equiangular map when \(\phi = -1\), and to the upper half of the equiangular map when \(\phi = 1 \). It is given by:

\[\Xi_{\mathrm{upper}} = (1 + \phi^2)\tan(\frac{\pi}{4}\frac{\xi+\phi}{1+\phi^2})-\phi\]

For \(\phi=0\) this generalized map simplifies to the original equiangular map \(\Xi_0 = \tan(\frac{\pi}{4}\xi)\).

This function is compatible with the ability to bulge out the Frustum; the map and Jacobian remain unchanged, modulo this substitution.

Constructor & Destructor Documentation

Frustum()

domain::CoordinateMaps::Frustum::Frustum	(	const std::array< std::array< double, 2 >, 4 > &	face_vertices,
		double	lower_bound,
		double	upper_bound,
		OrientationMap< 3 >	orientation_of_frustum,
		bool	equiangular_map_at_outer = false,
		bool	equiangular_map_at_inner = false,
		Distribution	zeta_distribution = Distribution::Linear,
		std::optional< double >	distribution_value = std::nullopt,
		double	sphericity = 0.0,
		double	transition_phi = 0.0,
		double	opening_angle = M_PI_2
	)

Constructs a frustum.

Parameters

face_vertices	An array of four 2D vertices that define the (x, y) coordinates of the upper and lower base of the frustum.
lower_bound	z distance from the origin to the lower base of the frustum.
upper_bound	z distance from the origin to the upper base of the frustum.
orientation_of_frustum	The orientation of the frustum in 3D space.
equiangular_map_at_outer	Determines whether to apply a tangent function mapping to the logical coordinates (true) or not (false) at the larger side of the frustum.
equiangular_map_at_inner	Determines whether to apply a tangent function mapping to the logical coordinates (true) or not (false) at the smaller side of the frustum.
zeta_distribution	Whether to apply a linear, logarithmic, or projective mapping to the logical zeta coordinate.
distribution_value	In the case of a projective map, the projective scale factor, otherwise unused.
sphericity	Value between 0 and 1 which determines whether the surface of the upper base of the Frustum is flat (value of 0), spherical (value of 1), or somewhere in between.
transition_phi	Determines whether the equiangular map used conforms to a lower half wedge (value of -1), an upper half wedge (value of +1), or a full wedge (value of 0).
opening_angle	The opening angle of the wedge the frustum will conform to (have conforming boundaries with).

---

The documentation for this class was generated from the following file:

• src/Domain/CoordinateMaps/Frustum.hpp