Table of Contents
Domain Decomposition
The spatial domain on which the solution is computed is divided into non-overlapping cells. For 2D and 3D domains, we use curvilinear quadrilateral and curvilinear hexahedral elements, respectively. The specification of a particular spatial domain is given by the DomainCreator. DomainCreators specify the properties of the initial elements (before AMR takes place), which are then used by Domain to create Blocks. Each Block holds a CoordinateMap (described below) as well as information about its neighbors. For geometrical domains, (e.g. rectilinear, spherical) there are a few shortcuts that can be used such that a user does not need to specify by hand the map and neighbor information for each Block; these methods are explained below.
CoordinateMaps
Each Block in the Domain must hold a CoordinateMap which describes how to map the logical cube (a reference cell that covers the interval \([-1, 1]\) in each dimension) to the curvilinear hexahedral element the Block describes. The CoordinateMap also provides the jacobian of the mapping.
Shortcuts for CoordinateMaps
For spherical domains, Wedge<3> implements the cubed-sphere map, and there exists the method sph_wedge_coordinate_maps in Domain/DomainHelpers.hpp to quickly construct six of these maps at once. For rectilinear multicube domains, Affine and Equiangular map the logical cubes to cartesian cubes. The method maps_for_rectilinear_domains in DomainHelpers allows the user to obtain the CoordinateMaps for all of the Blocks in such a domain at once. These can both be used to provide the map arguments to the Domain constructor.
Boundary Information
Each Block must know which of the other Blocks in the Domain are its neighbors and which of its logical directions points to an external boundary.
Shortcuts for Boundary Information
A quick way to encode the neighbor and boundary information for the blocks in a domain is through our convention of numbering and ordering the corners of the blocks in a well-defined way. The corner numbering scheme is described in the OrientationMap tutorial. For spherical domains, DomainHelpers has the methods corners_for_radially_layered_domains and corners_for_biradially_layered_domains, which provides the proper corner numberings for the maps obtained from the method sph_wedge_coordinate_maps. These methods are used in the Sphere DomainCreator. For rectilinear multicube domains, DomainHelpers has the methods corners_for_rectilinear_domains, which provides the proper corner numberings for the maps obtained from the method maps_for_rectilinear_domains.
Creating Rectilinear Domains with Shortcuts:
The construction of a rectilinear domain begins with the specification of the total extents of the domain in each cartesian direction, in terms of the number of blocks. These extents are held in an Index object. For an illustrative example, we will explain how to construct a cubical domain which has an extent of two blocks in each dimension:
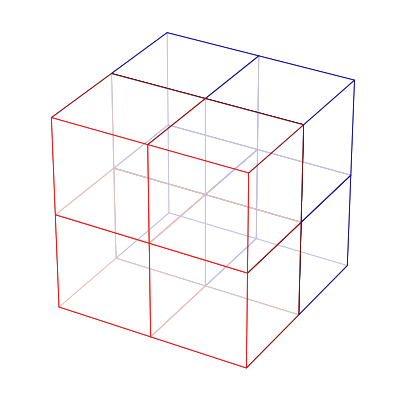
The first step is to generate the corner numbering for this Domain. For the purposes of this example, we will construct all blocks with their logical directions aligned with one another. As each block must also have an associated block id, we must be aware of the order in which the corners for each block are constructed.
The algorithm corners_for_rectilinear_domains always begins with the block located in the lowest cartesian corner of the domain. The second block is its immediate neighbor in the \(+x\) direction, and so on until the block in this row with the highest \(x\) coordinate is reached. The next block is the the immediate neighbor of the lowest corner block in the \(+y\) direction, and then continues through the neighboring blocks in the \(+x\) as before. This is the same order in which the global corners numbers are assigned to the vertices of the blocks.
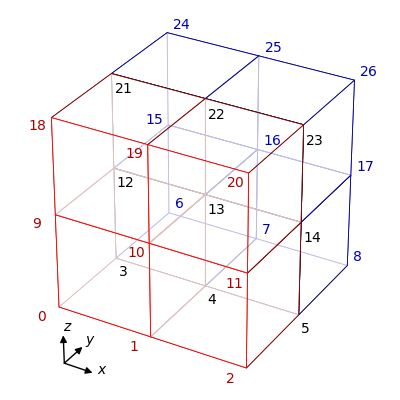
The block corners generated by corners_for_rectilinear_domains are then:
What remains is to specify the CoordinateMaps that each Block will hold. This is handled by maps_for_rectilinear_domains and currently supports both Affine and Equiangular mappings. The coordinate extents of each map is set by the argument to block_demarcations. For a 2x2x1 domain, the call to maps_for_rectilinear_domains could be:
For this choice of arguments we obtain the maps for a domain that extends from 0.0 to 2.0 in the \(x\)-direction, from 0.0 to 2.0 in the \(y\) -direction, and from -0.4 to 0.3 in the \(z\) direction.
With the corners and maps in hand, we can pass these as arguments to the Domain constructor.
Non-trivial Domain Example
The aforementioned functions can also take an additional argument to exclude blocks from a domain. For this one needs to know the Index<Dim> for each block they wish to exclude from the domain. For the 2x2x2 domain example, the block indices are:
In this example, we construct a domain with topology \(S^3\), which begins with the net for a tesseract. We begin by specifying that the domain extents are three blocks along the \(x\) and \(y\) directions, and four blocks along the \(z\) direction. In addition, we exclude the following block indices:
Alternatively, we can exclude none of the blocks in this way and instead selectively copy the block corners from the returned vector into a new vector that only contains the corners for the desired blocks, if one prefers to work with single-number array indices as opposed to tuples.
Either way, we end up with a vector of block corners corresponding to the following diagram:
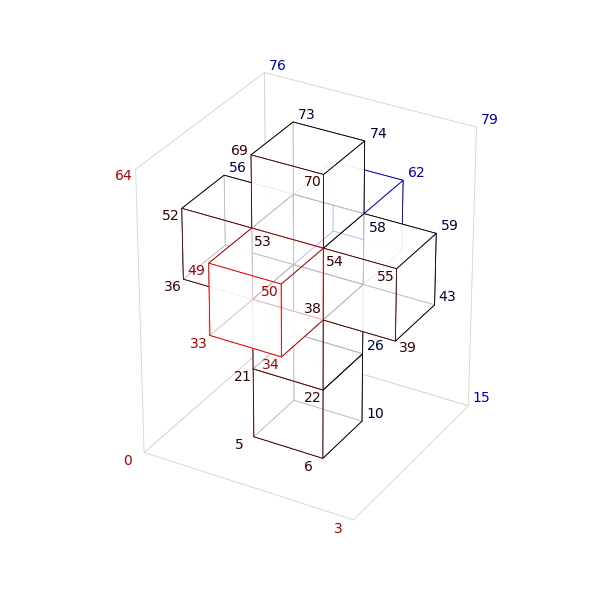
The maps are obtained similarly. In this case we suggest using the Equiangular maps for this Domain since they adapt the logical coordinates to the angular coordinates on a sphere. We also need to identify corresponding faces with each other to obtain a domain of topology \(S^3\), so we also need to supply the constructor of Domain with PairsOfFaces. For the \(S^3\) domain, these faces are: