Redistributes gridpoints within the unit sphere. More...
#include <SpecialMobius.hpp>
Public Member Functions | |
| SpecialMobius (double mu) | |
| SpecialMobius (SpecialMobius &&)=default | |
| SpecialMobius (const SpecialMobius &)=default | |
| SpecialMobius & | operator= (const SpecialMobius &)=default |
| SpecialMobius & | operator= (SpecialMobius &&)=default |
| template<typename T > | |
| std::array< tt::remove_cvref_wrap_t< T >, 3 > | operator() (const std::array< T, 3 > &source_coords) const |
| std::optional< std::array< double, 3 > > | inverse (const std::array< double, 3 > &target_coords) const |
| Returns std::nullopt for target_coords outside the unit sphere. The inverse function is only callable with doubles because the inverse might fail if called for a point out of range, and it is unclear what should happen if the inverse were to succeed for some points in a DataVector but fail for other points. | |
| template<typename T > | |
| tnsr::Ij< tt::remove_cvref_wrap_t< T >, 3, Frame::NoFrame > | jacobian (const std::array< T, 3 > &source_coords) const |
| template<typename T > | |
| tnsr::Ij< tt::remove_cvref_wrap_t< T >, 3, Frame::NoFrame > | inv_jacobian (const std::array< T, 3 > &source_coords) const |
| void | pup (PUP::er &p) |
| bool | is_identity () const |
Static Public Attributes | |
| static constexpr size_t | dim = 3 |
Friends | |
| bool | operator== (const SpecialMobius &lhs, const SpecialMobius &rhs) |
Detailed Description
Redistributes gridpoints within the unit sphere.
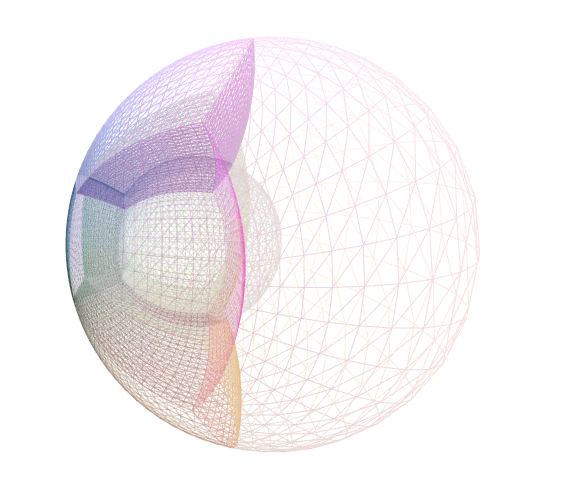
Details
A special case of the conformal Mobius transformation that maps the unit ball to itself. This map depends on a single parameter, mu \( = \mu\), which is the x-coordinate of the preimage of the origin under this map. This map has the fixed points \(x=1\) and \(x=-1\). The map is singular for \(\mu=1\) but we have found that this map is accurate up to 12 decimal places for values of \(\mu\) up to 0.96.
We define the auxiliary variables
\[ r := \sqrt{x^2 + y^2 +z^2}\]
and
\[ \lambda := \frac{1}{1 - 2 x \mu + \mu^2 r^2}\]
The map corresponding to this transformation in cartesian coordinates is then given by:
\[\vec{x}'(x,y,z) = \lambda\begin{bmatrix} x(1+\mu^2) - \mu(1+r^2)\\ y(1-\mu^2)\\ z(1-\mu^2)\\ \end{bmatrix}\]
The inverse map is the same as the forward map with \(\mu\) replaced by \(-\mu\).
This map is intended to be used only inside the unit sphere. A point inside the unit sphere maps to another point inside the unit sphere. The map can have undesirable behavior at certain points outside the unit sphere: The map is singular at \((x,y,z) = (1/\mu, 0, 0)\) (which is outside the unit sphere since \(|\mu| < 1\)). Moreover, a point on the \(x\)-axis arbitrarily close to the singularity maps to an arbitrarily large value on the \(\pm x\)-axis, where the sign depends on which side of the singularity the point is on.
A general Mobius transformation is a function on the complex plane, and takes the form \( f(z) = \frac{az+b}{cz+d}\), where \(z, a, b, c, d \in \mathbb{C}\), and \(ad-bc\neq 0\).
The special case used in this map is the function \( f(z) = \frac{z - \mu}{1 - z\mu}\). This has the desired properties:
- The unit disk in the complex plane is mapped to itself.
- The x-axis is mapped to itself.
- \(f(\mu) = 0\).
The three-dimensional version of this map is obtained by rotating the disk in the plane about the x-axis.
This map is useful for performing transformations along the x-axis that preserve the unit disk. A concrete example of this is in the BBH domain, where two BBHs with a center-of-mass at x= \(\mu\) can be shifted such that the new center of mass is now located at x=0. Additionally, the spherical shape of the outer wave-zone is preserved and, as a mobius map, the spherical coordinate shapes of the black holes is also preserved.
The documentation for this class was generated from the following file:
- src/Domain/CoordinateMaps/SpecialMobius.hpp