Redistributes gridpoints on the sphere. More...
#include <EquatorialCompression.hpp>
Public Member Functions | |
| EquatorialCompression (double aspect_ratio, size_t index_pole_axis=2) | |
| EquatorialCompression (EquatorialCompression &&)=default | |
| EquatorialCompression (const EquatorialCompression &)=default | |
| EquatorialCompression & | operator= (const EquatorialCompression &)=default |
| EquatorialCompression & | operator= (EquatorialCompression &&)=default |
| template<typename T > | |
| std::array< tt::remove_cvref_wrap_t< T >, 3 > | operator() (const std::array< T, 3 > &source_coords) const |
| std::optional< std::array< double, 3 > > | inverse (const std::array< double, 3 > &target_coords) const |
| The inverse function is only callable with doubles because the inverse might fail if called for a point out of range, and it is unclear what should happen if the inverse were to succeed for some points in a DataVector but fail for other points. | |
| template<typename T > | |
| tnsr::Ij< tt::remove_cvref_wrap_t< T >, 3, Frame::NoFrame > | jacobian (const std::array< T, 3 > &source_coords) const |
| template<typename T > | |
| tnsr::Ij< tt::remove_cvref_wrap_t< T >, 3, Frame::NoFrame > | inv_jacobian (const std::array< T, 3 > &source_coords) const |
| void | pup (PUP::er &p) |
| bool | is_identity () const |
Static Public Attributes | |
| static constexpr size_t | dim = 3 |
Friends | |
| bool | operator== (const EquatorialCompression &lhs, const EquatorialCompression &rhs) |
Detailed Description
Redistributes gridpoints on the sphere.
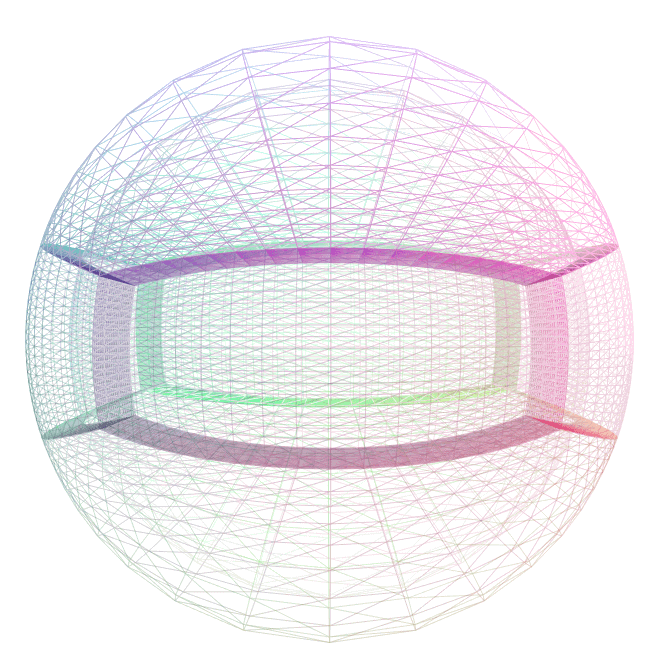
Details
A mapping from the sphere to itself which redistributes points towards (or away from) a user-specifed axis, indicated by index_pole_axis_. Once the axis is selected, the map is determined by a single parameter, the aspect_ratio \(\alpha\), which is the ratio of the distance perpendicular to the polar axis to the distance along the polar axis for a given point. This parameter name was chosen because points with \(\tan \theta = 1\) get mapped to points with \(\tan \theta' = \alpha\). In general, gridpoints located at an angle \(\theta\) from the pole are mapped to a new angle \(\theta'\) satisfying \(\tan \theta' = \alpha \tan \theta\).
For an aspect_ratio greater than one, the gridpoints are mapped towards the equator, leading to an equatorially compressed grid. For an aspect_ratio less than one, the gridpoints are mapped towards the poles. Note that the aspect ratio must be positive.
Suppose the polar axis were the z-axis, given by index_pole_axis_ == 2. We can then define the auxiliary variables \( r := \sqrt{x^2 + y^2 +z^2}\) and \( \rho := \sqrt{x^2 + y^2 + \alpha^{-2} z^2}\).
The map corresponding to this transformation in cartesian coordinates is then given by:
\[\vec{x}'(x,y,z) = \frac{r}{\rho}\begin{bmatrix} x\\ y\\ \alpha^{-1} z\\ \end{bmatrix}.\]
The mappings for polar axes along the x and y axes are similarly obtained.
The documentation for this class was generated from the following file:
- src/Domain/CoordinateMaps/EquatorialCompression.hpp