Visualization with Python

This tutorial shows you how to load 3D volume data in Python and visualize it using matplotlib.

First, you need access to the spectre Python bindings. A simple way to do this is to run a Jupyter server from the build directory:

./bin/python-spectre -m jupyterlab

You can find detailed instruction in the tutorial on Using SpECTRE's Python modules.

‍Note for VSCode users: You can also select this Jupyter server as kernel for notebooks running in VSCode (see docs).

Now we can import modules from the spectre Python package.

# Distributed under the MIT License.
# See LICENSE.txt for details.
 
import matplotlib.pyplot as plt
import numpy as np
import os
 
plt.style.use("../Examples/plots.mplstyle")

Select an observation

First, we open the H5 volume data files from a simulation and get a list of all available observations and their times:

from spectre.IO.H5 import list_observations, open_volfiles
import glob
 
h5files = glob.glob(
    # Point this to your volume data files
    "BbhVolume*.h5"
)
subfile_name = "/VolumeData"
obs_ids, obs_times = list_observations(open_volfiles(h5files, subfile_name))

We can also list all available variables in the volume data files:

import rich.columns
 
for volfile in open_volfiles(h5files, subfile_name, obs_ids[-1]):
    all_vars = volfile.list_tensor_components(obs_ids[-1])
    # Only look into the first file. The other should have the same variables.
    break
 
rich.print(rich.columns.Columns(all_vars))

ConformalFactor                 ExtrinsicCurvature_xx           ExtrinsicCurvature_yx          
ExtrinsicCurvature_yy           ExtrinsicCurvature_zx           ExtrinsicCurvature_zy          
ExtrinsicCurvature_zz           InertialCoordinates_x           InertialCoordinates_y          
InertialCoordinates_z           Lapse                           RadiallyCompressedCoordinates_x
RadiallyCompressedCoordinates_y RadiallyCompressedCoordinates_z ShiftExcess_x                  
ShiftExcess_y                   ShiftExcess_z                   Shift_x                        
Shift_y                         Shift_z                         SpatialMetric_xx               
SpatialMetric_yx                SpatialMetric_yy                SpatialMetric_zx               
SpatialMetric_zy                SpatialMetric_zz                                               

Interpolate to a slice

One way of visualizing your 3D volume data in a 2D plot is with a slice. Use interpolate_to_points to interpolate your volume data to any set of coordinates:

from spectre.IO.Exporter import interpolate_to_points
 
# Coordinates of a regular grid in the xy plane
x, y = np.meshgrid(np.linspace(-15, 15, 300), np.linspace(-15, 15, 300))
z = np.zeros(x.shape)
 
# Interpolation can be slow, so it's useful to cache the result. Remember to
# delete the cache file if you change anything.
cache_file = "interpolated_data.npy"
if os.path.isfile(cache_file):
    lapse = np.load(cache_file)
else:
    lapse = np.array(
        interpolate_to_points(
            h5files,
            subfile_name=subfile_name,
            observation_id=obs_ids[-1],
            tensor_components=["Lapse"],
            target_points=[x.flatten(), y.flatten(), z.flatten()],
        )
    ).reshape(x.shape)
    np.save(cache_file, lapse)

Now we can plot the 2D slice with matplotlib:

# Plot lapse
plt.contourf(x, y, np.log(1 - lapse))
 
# Plot circles for black holes
ax = plt.gca()
for bh_pos in [-8, 8]:
    ax.add_patch(
        plt.Circle(xy=(bh_pos, 0), radius=0.89, color="black", fill=True)
    )
 
# Make plot square
ax.set_aspect("equal")

/var/folders/xp/5t2ny359187c4ljckf8sz3m80000gn/T/ipykernel_19858/3375439396.py:2: RuntimeWarning: invalid value encountered in subtract
  plt.contourf(x, y, np.log(1 - lapse))

png

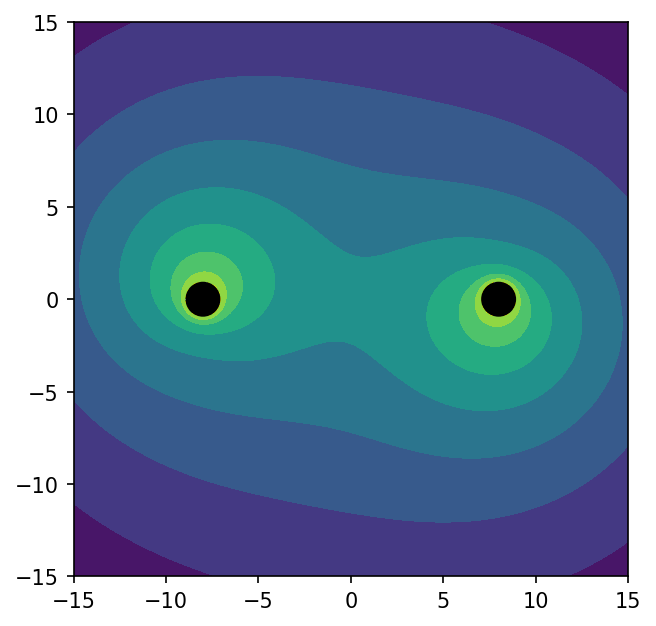
Plot individual elements

You can also iterate over elements in your volume data to plot things like element boundaries, collocation points, etc. Use iter_elements:

from spectre.IO.H5.IterElements import iter_elements
 
# Create a 3D plot
ax = plt.gcf().add_subplot(111, projection="3d")
ax.axis("off")
 
# Iterate over elements
for element in iter_elements(
    open_volfiles(h5files, subfile_name),
    obs_ids=obs_ids[0],
    element_patterns=["B3,*"],  # Only plot elements in block 3
):
    # Draw outline of the element by mapping the edges of the logical cube to
    # inertial coordinates using the element map
    for d in range(3):
        for edge in range(4):
            line = np.zeros((3, 100))
            line[d, :] = np.linspace(-1, 1, 100)
            line[(d + 1) % 3, :] = 2 * (edge % 2) - 1
            line[(d + 2) % 3, :] = 2 * (edge // 2) - 1
            x, y, z = element.map(line)
            ax.plot(x, y, z, color="black")
 
# Make plot square
ax.set_aspect("equal")

png

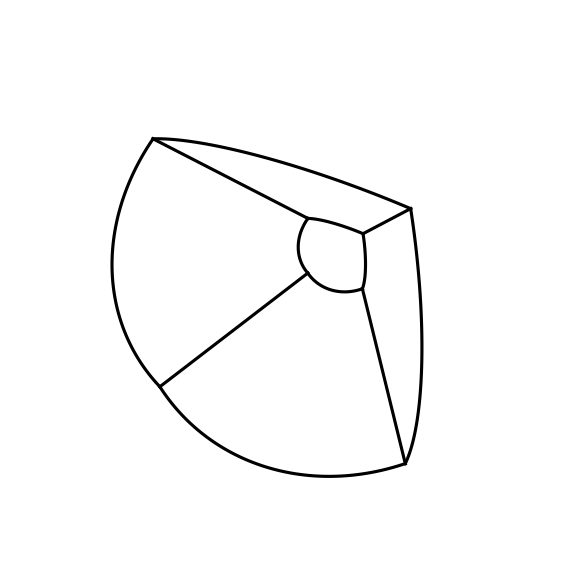
Transforming volume data

Often you want to post-process volume data to compute derived quantities from the ones the simulation has written out. You can sometimes do this within tools like ParaView (e.g. using ParaView's "Calculator" filter) if the computation is simple enough and pointwise (i.e., needs no derivatives or other mesh information). If you can't get what you need in ParaView, you can use spectre transform-vol. It takes any Python function (a "kernel"), runs it over your volume data, and writes the result back into the files.

For example, let's add the number of grid points in each element as a field that we can visualize:

spectre transform-vol BbhVolume*.h5 -d VolumeData \
    -k spectre.Spectral.Mesh3D:extents

You will be prompted to select an output dataset name (hit enter to select the default "Extents"). The result will be written back into the H5 files. If you now regenerate an XDMF file for the volume data you will be able to see the output in ParaView.

The transform-vol tool supports arbitrary Python functions as kernels. Many Python functions from the spectre module are useful kernels. For example, here are some useful kernels:

• p-refinement (number of grid points per dimension): spectre.Spectral.Mesh3D:extents
• Relative/absolute truncation error (from power monitors): spectre.NumericalAlgorithms.LinearOperators:relative_truncation_error or absolute_truncation_error
• Coordinates in different frames: Element:grid_coordinates or Element:distorted_coordinates

You can find more useful kernels by browsing the spectre.PointwiseFunctions module: https://spectre-code.org/py/_autosummary/spectre.PointwiseFunctions.html

You can also write your own kernels. Create a Python file, e.g. kernel.py, and write a function like this:

%%file kernel.py
from spectre.DataStructures.Tensor import Scalar, DataVector
 
def lapse_squared(lapse: Scalar[DataVector]) -> Scalar[DataVector]:
    return np.array(lapse)**2

Now you can run this kernel over your volume data like this:

spectre transform-vol BbhVolume*.h5 -d VolumeData \
    -e kernel.py -k lapse_squared

You can find more details by running spectre transform-vol --help.